化工学报, 2021, 72(3): 1769-1777 doi: 10.11949/0438-1157.20200749

过程安全

基于多源异构数据融合的化工安全风险动态量化评估方法

刘庆龙,1, 曲秋影2, 赵东风3, 刘尚志2, 王劲1

1.青岛欧赛斯环境与安全技术有限责任公司，山东 青岛 266520

2.中国石油大学（华东）机电工程学院，山东 青岛 266580

3.中国石油大学（华东）化学工程学院，山东 青岛 266580

Dynamic quantitative assessment method of chemical safety risk based on multi-source heterogeneous data fusion

LIU Qinglong,1, QU Qiuying2, ZHAO Dongfeng3, LIU Shangzhi2, WANG Jin1

1.Qingdao OASIS Environmental & Safety Technology Co. , Ltd. , Qingdao 266520, Shandong, China

2.College of Electromechanic Engineering, China University of Petroleum (East China), Qingdao 266580, Shandong, China

3.College of Chemical Engineering, China University of Petroleum (East China), Qingdao 266580, Shandong, China

通讯作者: 刘庆龙（1988—），男，硕士，高级工程师，lqlong2008@126.com

收稿日期: 2020-06-13   修回日期: 2020-07-20   网络出版日期: 2021-03-25

基金资助: 山东省重点研发计划重大科技创新工程.  2019JZZY020502
青岛市民生科技计划项目.  19-6-1-96-nsh

Received: 2020-06-13   Revised: 2020-07-20   Online: 2021-03-25

作者简介 About authors

刘庆龙（1988—），男，硕士，高级工程师，lqlong2008@126.com , E-mail：lqlong2008@126.com

摘要

针对石化企业过程安全风险分析缺乏多源异构数据融合、难以解析风险动态时变机理的现状。首先基于改进的模糊Petri网建立风险动态传播模型，考虑初始事件失效、保护层失效和修正因子等参数，得到风险的实时变化概率；然后分析不同保护层失效对事故发生概率的影响，得到不同保护层的重要程度；最后，以正己烷缓冲罐溢流发生火灾爆炸事故为例进行动态风险计算，分析对比其在不同保护层失效下的事故发生概率变化，结果表明安全联锁系统对事故发生起关键作用，日常应加大对其检测力度，防止事故发生。

关键词： 多源异构数据 ; 知识图谱 ; 过程系统 ; 集成 ; 安全

Abstract

In view of the lack of multi-source heterogeneous data fusion in process safety risk analysis of petrochemical enterprises, it is difficult to analyze the dynamic time-varying mechanism of risk. First, it is established a dynamic risk propagation model based on the improved fuzzy Petri net, consider parameters such as initial event failure, protection layer failure, and correction factors to obtain the real-time change probability of risk. Then the influence of failure of different protective layers on the probability of accidents is analyzed and the importance degree of different protective layers is obtained. Finally, taking n-hexane buffer tank overflow fire and explosion accident as an example, the dynamic risk calculation was carried out to analyze and compare the change of accident probability under the failure of different protective layers. The results showed that the safety interlock system played a key role in the accident, and the daily detection should be strengthened to prevent the accident.

Keywords： multi-source heterogeneous data ; knowledge map ; process system ; integration ; safety

PDF (1615KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

刘庆龙, 曲秋影, 赵东风, 刘尚志, 王劲. 基于多源异构数据融合的化工安全风险动态量化评估方法[J]. 化工学报, 2021, 72(3): 1769-1777. doi:10.11949/0438-1157.20200749

LIU Qinglong, QU Qiuying, ZHAO Dongfeng, LIU Shangzhi, WANG Jin. Dynamic quantitative assessment method of chemical safety risk based on multi-source heterogeneous data fusion[J]. CIESC Journal, 2021, 72(3): 1769-1777. doi:10.11949/0438-1157.20200749

引 言

石油化工行业是我国的支柱产业之一，对于推动我国经济发展发挥着重要作用。在化工生产过程中，通常包含大量易燃易爆及有毒有害的危险物质，伴随着高温、高压的生产环境，极易引发事故，发生灾难性后果。近年来，化工行业安全生产形势整体有所好转，但情况依然不容乐观[1]。因此，在石化企业中，评估过程系统的安全风险预测事故发生情况，将潜在的安全风险保持在风险可接受水平以下尤为重要。

传统的定量风险分析方法已较为成熟，但也存在许多缺陷，如事件树、事故树以及Bow-tie等方法[2-5]无法考虑基本事件之间的条件依赖性，并且其本质是静态的，无法更新事件概率以及随之而来的风险。近年来，贝叶斯网络被广泛应用于动态风险评估工作[6-8]，但其需要大量先验数据，而实际生产过程中历史故障数据的获取往往比较困难，使得该方法不易实施。符号有向图（SDG）是一种基于过程知识的因果性建模方法，该方法通过分析节点间关系及状态变化描述系统故障[9]，但其缺乏对故障路径的标记，在风险的动态传播方面缺乏直观性。模糊Petri网（FPN）是研究风险动态传播机理的有效手段，可建立各风险节点之间的联系，从而对初始事件到发生事故的演化过程进行直观分析，得到事故演化路径。目前已广泛应用于电网、交通、化工等领域[10-14]，但其在定量计算过程中数据都是通过数据库所得，并不能很好地反映实际工况。目前，很多企业已建立信息化管理平台，利用大数据、人工智能等对数据进行实时采集[15]，多源异构数据融合技术得到广泛应用[16-20]。

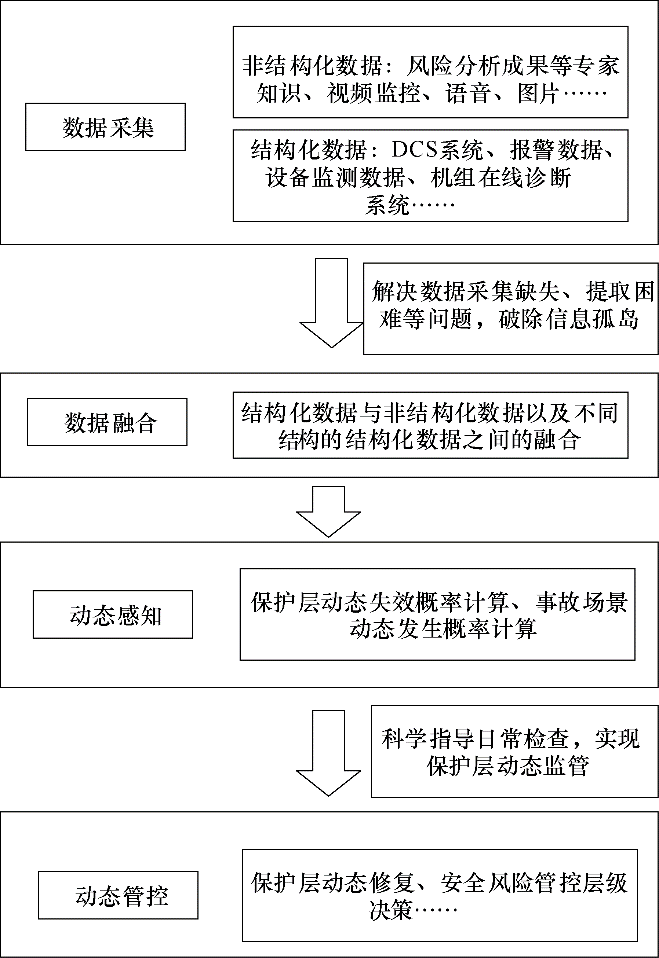
随着自动化、信息化、智能化等技术渗透到化工企业生产过程的各个环节，现场的传感器、生产过程中的各个信息系统均会产生大量数据，这些数据分布在多个数据源中，具有多源、异构的特点[21]。因此，针对目前风险分析缺乏数据融合，难以解析风险动态时变机理的现状。本文采用知识图谱处理非结构化数据，在此基础上进一步融合设备监测数据、报警数据等结构化数据，利用多源异构数据的关联、交叉和融合，采用HAZOP+LOPA分析的方法分析事故后果场景，建立基于改进模糊Petri网的因果链路拓扑，进而充分考虑失效和故障数据随时间的变化，解析风险动态时变机理，最终建立动态风险量化评估模型，该模型的数据融合架构如图1所示，能够实时定量评估事故场景发生概率，精准测量风险点动态风险值，并分析不同保护层失效时风险的动态变化，科学指导安全风险管控措施的日常检查、维护及定期测试。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   多源异构数据融合架构

Fig.1   Multi-source heterogeneous data fusion architecture


1 模糊Petri网基本原理

模糊Petri网是Petri网的改进，将传统Petri网融合模糊集理论可以表示不确定性专家知识，进而对具有不确定性的专家系统进行建模[22]。考虑到炼化系统风险传播过程中有相应的保护层阻止事故发生，在传统模糊Petri网中故障库所的基础上加入保护层库所，表示系统中存在的保护层。将改进的模糊Petri网定义为一个九元组：{P,L,T,F,IN,OUT,W,V,D}，其中：

（1）P={p1,p2,p3,…,pi}表示故障库所集，即系统中存在的故障，i表示故障个数；

（2）L={l1,l2,l3,…,ln}表示保护层库所，即系统中存在的保护层，n表示保护层个数；

（3）T={t1,t2,t3,…,tm}表示变迁集，即某个风险的发生过程，m表示变迁的个数；

（4）F= {f1,f2,f3,…,fi}表示命题集，与pi相互对应；

（5）IN为P→T输入函数，表示输入库所到变迁的映射；

（6）OUT为T→P输出函数，表示变迁到输出库所的映射；

（7）W为权函数，表示库所p对变迁t成立的支持度；

（8）V={μ1,μ2,μ3,…,μm}表示故障库所及保护层库所的可信度集合，即设备发生故障的可能性；

（9）D={d1,d2,d3,…,dm}表示变迁发生的阈值集合，即变迁t发生必须满足wi×μ1≥d1。

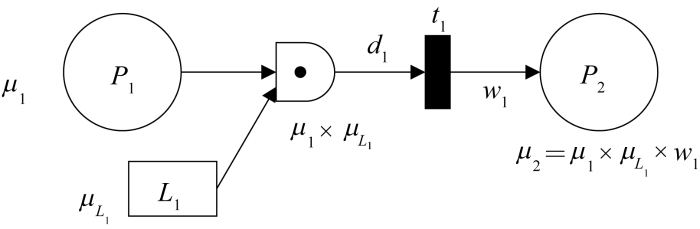
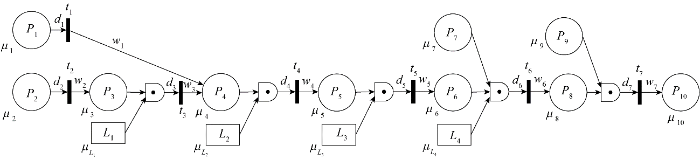
模糊Petri网能有效传承专家知识，通过因果拓扑直观展示HAZOP和LOPA风险分析成果等非结构化数据，进而融合控制系统故障数据、报警数据等结构化数据进行定量计算，并根据监测数据的波动实现事故场景概率的动态更新。以炼化系统中储罐溢流为例，对其建立改进的模糊Petri网模型，如图2所示。故障库所P1表示人员误开大阀，可信度μ1表示人员误开大阀的可能性，保护层库所L1表示液位控制系统失效，可信度μL1表示其发生故障的可能性，变迁t1表示引起储罐液位升高，发生变迁t1的阈值和权值分别为d1和w1，故障库所P2表示储罐的液位升高，可信度μ2表示储罐液位升高的可能性，若μ1×μL1>d1，变迁t1发生，μ2=μ1×μL1×w1；若μ1×μL1<d1，变迁t1不发生。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   模糊Petri网模型

Fig.2   Fuzzy Petri net model


2 动态量化评估模型建立

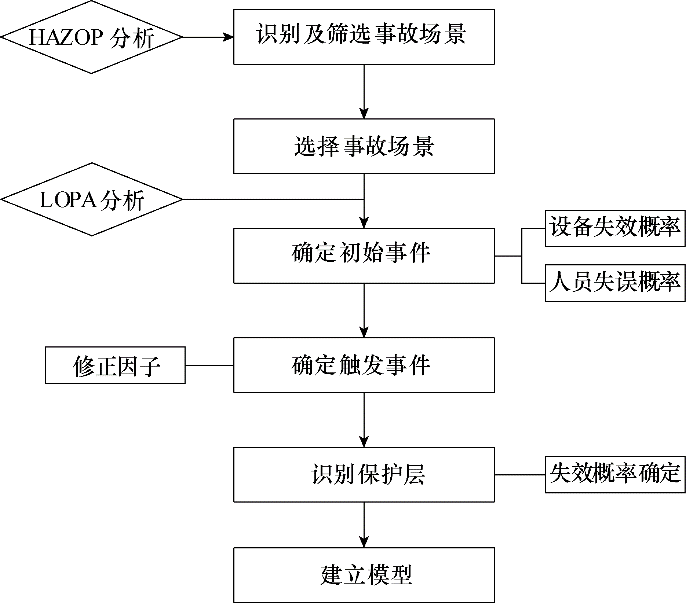
基于模糊Petri网的基本原理及相关关系，分析步骤如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   改进模糊Petri网的分析步骤

Fig.3   Improved analytical procedure diagram of fuzzy Petri net


（1） 识别及筛选事故场景

通过HAZOP分析确定初始（固有）风险等级较高的风险，进而采用LOPA分析进行事故场景分析，得出造成事故发生的原因、后果及措施。

（2） 确定初始事件及触发事件

触发事件包括使能条件和修正因子。修正因子通常包括点火概率、人员暴露概率、死亡率等[22]，着重对点火概率取值进行研究。

（3） 识别保护层

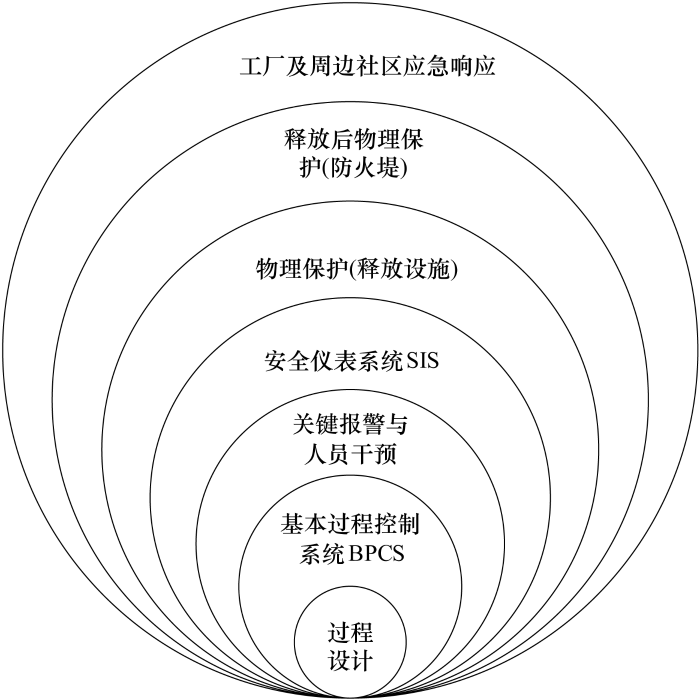
典型化工装置的保护层呈“洋葱形”分布，如图4所示[23]。本次研究主要针对基本过程控制系统（BPCS）、关键报警与人员干预、安全仪表系统（SIS）、物理保护、释放后物理保护等保护层进行分析。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   洋葱模型

Fig.4   The onion model


（4） 建立模糊Petri网模型

基于前面确立的事故场景以及分析得出的初始事件、触发事件和保护层，确定模型中的库所和变迁，根据化工过程故障传播的模糊Petri网表示规则，建立模型。

3 参数分析

3.1 初始事件失效分析

初始事件包括机械设备失效、控制系统故障、人员失误和外部事件。外部事件一般为自然环境引起的破坏事件，本次分析不做考虑。

（1） 机械设备失效和控制系统故障

现有设备失效概率取值大部分来源于国外数据库，如海上设备可靠性数据库（OREDA）、过程设备可靠性数据库（PERD）等，所选取的参照数据未结合我国设备使用实际情况。为获得更符合企业实际情况的设备失效概率，将设备失效分为两类：机械设备失效和BPCS控制系统故障。

BPCS控制系统故障定量计算方法可参照定量SIS的相关方法，采用式（1）计算控制系统每个部分的PFDavg，然后采用式（2）计算整个控制系统的故障概率PFDavgBPCS。

PFDavg=λDD×RT+λDU×TI2
PFDavgBPCS=PFDavgS+PFDavgL+PFDavgSE

式中，λDD表示检测到的子系统中危险失效率；RT表示平均维修时间；TI表示测试周期；λDU表示未检测到的子系统中危险失效率；PFDavgBPCS表示控制系统的故障概率；PFDavgS表示传感器子系统的失效概率；PFDavgL表示逻辑子系统的失效概率；PFDavgSE表示最终元件子系统的失效概率。

机械设备失效按照式（3）计算失效概率F[24]：

F=FG×FE×FM×FL

式中，FG表示同类设备的平均失效概率；FE表示设备修正系数；FM表示管理系统评价系数；FL表示超标缺陷影响系数。

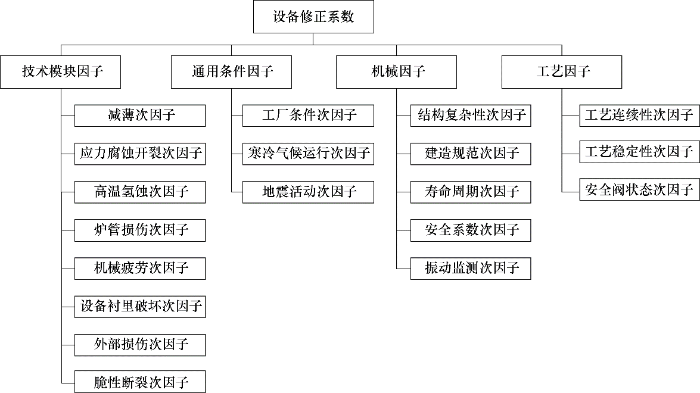
FE由四个因子组成（图5），需分别确定四个因子的取值后确定FE，FL根据设备的制造质量和服役过程中的退化机理来确定。因此，对于同一个工厂，FG和FM的取值是固定值，影响设备失效概率的主要是FE和FL。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   设备修正系数

Fig.5   Equipment correction factor


FE中四个因子的取值可通过监测介质的温度、压力、流速等运行数据以及企业的管理水平和设备的基础资料来确定，进而得出FE的取值。FL可通过设备的定期检验、服役条件等进行赋值。

通过对工厂中设备运行数据的监控不断更新设备的失效概率，实现机械设备失效概率的动态计算。

（2） 人员失误

目前应用较多的人因可靠性分析方法有THERP、CREAM、HCR、HEART、SLIM等[25-26]。为了更好地应用于各生产领域并获得更加精确的结果，本文融合THERP和HCR两种模型计算人员失误概率。

THERP模型是根据事故的发展过程，分析涉及的人员行为，建立人因可靠性事件树，并对树中各分支赋予其发生的概率，最终计算作业成功或失败的概率。

HCR模型是量化操作人员对系统异常信号没有在规定的时间完成规定指令的概率的模型[27]。计算公式如下：

P(t)=exp-βt/T1/2-γα

式中，t表示允许操作人员响应的时间；T1/2表示响应时间中值；α、β、γ表示与行为类别有关的威布尔分布参数。

T1/2的计算公式如下：

T1/2=T1/2,nominal(1+K1)(1+K2)(1+K3)

式中，T1/2,nominal表示一般状况的响应时间；K1表示操作人员经验；K2表示操作心理压力；K3表示控制室人机界面质量。

THERP模型主要针对与时间无关的人的序列动作；HCR模型则侧重于与时间相关的人的认知行为。人的行为一般包括认知、诊断和操作三个阶段。人员在认知及诊断阶段采用HCR方法选取相应的计算参数进行计算；用THERP方法来计算在操作阶段中人员失误概率，建立人因事件树进行分析。THERP+HCR模型综合了两种方法各自的优势对人因可靠性进行定量计算，为风险分析提供精确数据。

3.2 保护层失效分析

保护层可有效阻止初始事件进一步演化为事故，避免重大事故的发生。保护层中涉及到的设备失效概率可参照初始事件设备失效概率计算方法。

安全仪表系统保护层针对不同的冗余结构有不同的失效概率计算方法[28]，选取典型结构2oo3结构进行分析。2oo3结构是由三个并联通道构成，两个或两个以上通道发生危险失效时，则某个安全功能失效。该结构的平均要求时PFDavg2oo3计算公式如下：

PFDavg2oo3=61-βDλDD+1-βλDU2tCEtGE+βDλDDMTTR+βλDUTI2+MTTR

式中，β表示共因失效因子；λDU表示未检测到的子系统中危险失效率；βD表示诊断共因失效因子；λDD表示检测到的子系统中危险失效率；λSD表示检测到的子系统中安全失效率；tCE表示通道失效状态的平均时间；tGE表示系统等效停止工作时间；TI表示测试周期；MTTR表示平均恢复时间。

关键报警和人员干预保护层失效包括报警器失效和人员失误，其中报警器失效概率Pa按照设备的失效概率计算方法来计算，人员失误Pb包括操作员对报警的感知以及处理能力，对于这部分的人因可靠性计算，首先采用APRIORI算法挖掘报警事件与操作事件的关联关系[29]，根据报警数据计算人员的感知能力和处理能力，获得人因可靠性，进而获得人因失效概率。

APRIORI算法是挖掘关联规则的频繁项集算法，其实现过程如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   APRIORI算法实现过程

Fig.6   APRIORI algorithm implementation process


设C={x1, x2,…,xi, v1, v2,…, vj}是包含过程报警和处理事件的项的集合，x和v分别为过程变量和操作变量。通过该算法，可建立x→v的关联规则，其表示当x发生报警时，v可抑制报警的发生。因此，可用操作员是否成功处理了过程报警来衡量其处理能力，即

v1→x1
v1→x1→0

式（7）和式（8）分别表示操作员对报警处理成功和失败。

假设在统计期内产生的报警数量为M：

M=M1+M2
M1=M11+M12
M2=M21+M22

式中，M1表示仍然存在的报警；M2表示消失的报警；M11表示人员未响应仍存在的报警；M12表示人员响应但未消失的报警；M21表示人员未响应但消失的报警；M22表示人员响应后消失的报警。

其中，M1和M2根据统计数据获取，根据关联规则可分析得到M12和M22。

M12=I（v1→x1）

M22=I（v1→x1→0）

则操作员的感知能力计算公式为：

P1=M12+M22M

操作员的处理能力计算公式为：

P2=M22Iv1=Iv1→x1→0Iv1∈0,1      Iv1=01                                      Iv1≠0 

人因可靠性P′及人因失效率Pb计算公式如下：

P'=P1×P2
Pb=1-P1×P2

则关键报警和人员干预保护层失效概率P计算公式为：

P=Pa+Pb(1-Pa)

3.3 修正因子分析

点火概率指可燃物质泄漏后被点火源点燃的概率，分为立即点火概率和延迟点火概率。

立即点火概率默认值为0.15，该值极大地取决于泄漏物质特性及泄漏环境，因此应根据立即点火概率的主要影响因素得出更能反映实际情况的取值，考虑到泄漏物质本身的燃烧特性及泄漏环境得出其计算公式为[30]：

 Pimm.ignition=Pai+Psd=1-5000exp TTAIT-9.5+0.0024×145.04P13EMIE23

式中，Pai表示自燃特性概率；Psd表示点火能特性概率；Pimm.ignition表示立即点火概率；T表示泄漏物质的温度，℉；TAIT表示泄漏物质自燃温度，℉；EMIE表示泄漏物质最小点火能，mJ；P表示泄漏物质的压力，MPa。若T/TAIT<0.9，则Pai=0，若T/TAIT>1.2，则Pai=1。

延迟点火概率默认值为0.3，该值极大地取决于泄漏环境，应考虑物质的燃烧特性（Mmat）、物质的泄漏量（Mmag）、释放的持续时间及点火源强度（Mdur）、室内和户外运行（Min/out）四个修正系数对其进行修正[31]。

物质的燃烧特性：

Mmat=0.6-0.85lgMIE

式中，MIE为物质的最小点火能，mJ。Mmat的取值范围为0.1~3。

物质的泄漏量：

Mmag=7×exp0.642×ln FR-4.67

式中，FR为孔的流速，lbs/s（1kg/s=2.2lbs/s），最大值为2。

释放的持续时间及点火源强度：

Mdur=1-1-S2×e-0.015×St/0.3

式中，t表示时间，s。S为点火强度，取值可参照基于BakerRisk收集的数据[30]。

对于室内和户外运行（Min/out），一般考虑室外气体云的影响，若操作在室内，则Min/out=2，在室外则不需要考虑这个修正因子。

将以上四个参数的乘积（∏M）对延迟点火概率进行修正，具体计算方法如下：

Pdelayed ignition=1-[0.7/(∏M)] ,  ∏M>1
Pdelayed ignition=0.3×∏M,  ∏M<1

4 实例分析

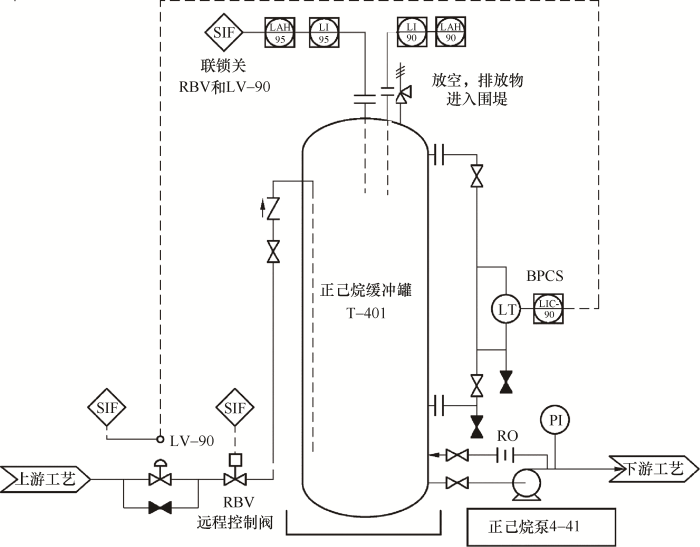
正己烷从上游工艺单元进入正己烷缓冲罐T-401，其简化流程如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   正己烷缓冲罐工艺流程图

Fig.7   Process flow chart of n-hexane buffer tank


（1）基于HAZOP分析结果，确定正己烷缓冲罐溢流事故场景，得出风险传播过程的初始事件、触发事件及相应的保护层，构建改进的模糊Petri网模型，如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   正己烷缓冲罐溢流事故模糊Petri网模型

Fig.8   Fuzzy Petri net model of overflow accident of n-hexane buffer tank


（2）模型中初始库所包括故障库所P1，P2，P7，P9和保护层库所L1，L2，L3，L4。初始库所的可信度根据企业历史运行数据，按照各参数计算方法，分析计算得出其取值，各变迁的权值和阈值由专家经验得出[14]，模型中各参数含义及取值见表1。

表1   模糊Petri网模型中各参数含义及取值

Table 1  The meaning and value of each parameter in fuzzy Petri net model

库所P变迁t
P含义可信度μt含义权值w阈值d
P1液位控制系统LIC-90故障8.66×10-2t1引起正己烷缓冲罐液位高0.900.003
P2人员误开大阀LV-902.01×10-2t2引起进料量增多0.950.002
P3进料量增多—t3引起正己烷缓冲罐液位高0.900.004
P4正己烷缓冲罐液位高—t4引起正己烷缓冲罐液位高高0.950.001
P5正己烷缓冲罐液位高高—t5引起正己烷缓冲罐溢流0.970.0005
P6正己烷缓冲罐溢流—t6引起火灾爆炸事故0.990.0001
P7点火6.40×10-1t7引起人员伤亡10.0001
P8火灾爆炸事故—
P9人员暴露5.00×10-1
P10人员伤亡—
L1液位控制系统LIC-90故障8.66×10-2
L2液位高报警及人员响应失效8.24×10-2
L3液位高高联锁失效2.01×10-2
L4防火堤失效1.30×10-2

新窗口打开| 下载CSV


经过对模型进行计算，得到缓冲罐溢流的发生概率为1.21×10-4，根据点火概率计算公式，得到其点火概率为0.64，人员暴露概率定为0.5，得到发生火灾爆炸概率及人员伤亡概率分别为9.99×10-7和4.99×10-7。根据风险矩阵，风险处于可接受范围。

基于目前保护层数量庞杂的现状，企业难以科学、全面地辨识逐个保护层的安全状态，因此，分别计算该模型在BPCS控制系统故障、关键报警及人员干预失效以及安全联锁系统分别失效、关键报警及人员干预和安全联锁系统同时失效时对事故发生的影响，为日常检查提供依据，计算结果如表2所示。

表2   各保护层失效事故发生概率

Table 2  Probability of failure accident of each protective layer

保护层失效缓冲罐溢流概率火灾爆炸概率人员伤亡概率
液位控制系统LIC-90故障1.40×10-31.15×10-55.77×10-6
液位高报警及人员响应失效1.47×10-31.21×10-56.06×10-6
液位高高联锁失效6.03×10-34.96×10-52.48×10-5
液位高报警及人员响应和液位高高联锁同时失效7.32×10-26.03×10-43.01×10-4

新窗口打开| 下载CSV


由计算结果可知，液位控制系统和液位高报警及人员响应失效对事故发生影响不大；安全联锁失效后，人员伤亡发生概率数量级发生明显变化，液位高报警和安全联锁同时失效后，风险处于不可接受范围。因此，该装置在日常检查过程中应加强对安全联锁系统的检测，确保其功能正常，防止事故发生。

另一方面，根据人员伤亡概率的目标概率，可以反算联锁等保护层的期望失效概率，进而得到测试周期等参数，科学指导保护层的动态完好性管理。

5 结 论

（1）基于现有的LOPA模型对事故场景进行分析，建立了考虑保护层的模糊Petri网模型，分析风险的动态传播路径。采用数据融合的方法作为信息收集手段，针对模型中涉及到的各种参数进行分析计算，构建多源数据融合的安全风险计算模型，分析结果表明其计算结果更为精确。

（2）以正己烷缓冲罐为例，建立其风险动态转移模型，通过对各参数分析计算得到其缓冲罐溢流事故、火灾爆炸事故及人员伤亡事故的发生概率。进一步分析其在不同保护层失效时的事故发生概率，结果表明安全联锁系统失效对事故发生影响最大，日常管理中应加大对其检测频率。另一方面，根据人员伤亡概率的目标概率，可以反算联锁等保护层的期望失效概率，进而得到测试周期等参数，科学指导保护层的动态完好性管理。

（3）基于多源数据融合的安全风险动态量化评估方法计算结果更加精确，能够反映系统实时风险，为过程安全管理提供有效依据。

参考文献

赵岩, 徐建华.

我国石油化工行业事故风险分析

[J]. 北京大学学报(自然科学版), 2018, 54(4): 857-864.

[本文引用: 1]

Zhao Y, Xu J H.

Analysis of accident risk in China's petrochemical industry

[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2018, 54(4): 857-864.

[本文引用: 1]

姚成玉, 王传路, 陈东宁, 等.

连续时间T-S动态故障树分析方法

[J]. 机械工程学报, 2020, 56(10): 244-256.

[本文引用: 1]

Yao C Y, Wang C L, Chen D N, et al.

Continuous-time T-S dynamic fault tree analysis method

[J]. Journal of Mechanical Engineering, 2020, 56(10): 244-256.

[本文引用: 1]

郭振东, 李金林, 王克巍, 等.

领结分析在收球系统安全管理中的应用

[J]. 化工进展, 2019, 38(S1): 259-264.

Guo Z D, Li J L, Wang K W, et al.

Bowtie analysis on pig launcher system safety management

[J]. Chemical Industry and Engineering Progress, 2019, 38(S1): 259-264.

Zhang L, Wu X, Skibniewski M J, et al.

Bayesian-network-based safety risk analysis in construction projects

[J]. Reliability Engineering & System Safety, 2014, 131: 29-39.

Xue L N, Fan J C, Rausand M, et al.

A safety barrier-based accident model for offshore drilling blowouts

[J]. Journal of Loss Prevention in the Process Industries, 2013, 26(1): 164-171.

[本文引用: 1]

Zarei E, Azadeh A, Aliabadi M M, et al.

Dynamic safety risk modeling of process systems using bayesian network

[J]. Process Safety Progress, 2017, 36(4): 399-407.

[本文引用: 1]

高妮, 高岭, 贺毅岳, 等.

基于贝叶斯攻击图的动态安全风险评估模型

[J]. 四川大学学报(工程科学版), 2016, 48(1): 111-118.

Gao N, Gao L, He Y Y, et al.

Dynamic security risk assessment model based on Bayesian attack graph

[J]. Journal of Sichuan University (Engineering Science Edition), 2016, 48(1): 111-118.

张子扬, 任翔, 吕成, 等.

基于贝叶斯模型的安全系统动态风险分析

[J]. 高校化学工程学报, 2015, 29(3): 642-649.

[本文引用: 1]

Zhang Z Y, Ren X, Lü C, et al.

Safety system dynamic failure assessment using Bayesian model simulation

[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(3): 642-649.

[本文引用: 1]

姜英, 王政, 秦艳, 等.

基于复杂网络的化工过程层次符号有向图模型建立及关键节点识别

[J]. 化工进展, 2018, 37(2): 444-451.

[本文引用: 1]

Jiang Y, Wang Z, Qin Y, et al.

AHP-SDG model establishment and key node identification of chemical process system based on complex network

[J]. Chemical Industry and Engineering Progress, 2018, 37(2): 444-451

[本文引用: 1]

Chen G H, Wang S K, Tan X Q.

Evaluation model for safety capacity of chemical industrial park based on acceptable regional risk

[J]. Chinese Journal of Chemical Engineering, 2015, 23(1): 121-127.

[本文引用: 1]

Liu H C, Liu L, Lin Q L, et al.

Knowledge acquisition and representation using fuzzy evidential reasoning and dynamic adaptive fuzzy Petri nets

[J]. IEEE Transactions on Cybernetics, 2013, 43(3): 1059-1072.

Zhang Y, Zhang Y, Wen F, et al.

A fuzzy Petri net based approach for fault diagnosis in power systems considering temporal constraints

[J]. International Journal of Electrical Power & Energy Systems, 2016, 78: 215-224.

吴鹏, 夏海波, 吴建军, 等.

基于模糊Petri网的易流态化货物海上运输风险评估

[J]. 上海海事大学学报, 2019, 40(3): 63-68.

Wu P, Xia H B, Wu J J, et al.

Risk assessment of shipping liquefiable solid bulk cargoes based on fuzzy Petri nets

[J]. Journal of Shanghai Maritime University, 2019, 40(3): 63-68.

胡瑾秋, 曹雅琴, 张来斌, 等.

考虑保护层响应的炼化过程系统风险动态转移模型

[J]. 中国安全科学学报, 2015, 25(3): 83-89.

[本文引用: 2]

Hu J Q, Cao Y Q, Zhang L B, et al.

Model considering response of protection layers for systematic risk dynamic transfer in refinery process

[J]. China Safety Science Journal, 2015, 25(3): 83-89.

[本文引用: 2]

胡瑾秋, 郭家洁.

基于尺度效应的过程安全事故概率估计

[J]. 化工学报, 2017, 68(12): 4848-4856.

[本文引用: 1]

Hu J Q, Guo J J.

Accident probability estimation of process safety based on scale effect

[J]. CIESC Journal, 2017, 68(12): 4848-4856.

[本文引用: 1]

华丽, 于海晨, 邵诚, 等.

基于SVM-BOXPLOT的乙烯生产过程异常工况监测与诊断

[J]. 化工学报, 2018, 69(3): 1053-1063.

[本文引用: 1]

Hua L, Yu H C, Shao C, et al.

Monitoring and diagnosis of abnormal condition in ethylene production process based on SVM-BOXPLOT

[J]. CIESC Journal, 2018, 69(3): 1053-1063.

[本文引用: 1]

李卫星, 王峰, 李智国, 等.

面向多源数据的军事信息系统设计

[J]. 中国电子科学研究院学报, 2020, 15(3): 237-243.

Li W X, Wang F, Li Z G, et al.

Design of military information system based on multi-source data

[J]. Journal of China Academy of Electronics and Information Technology, 2020, 15(3): 237-243.

窦珊, 张广宇, 熊智华, 等.

基于多源数据融合的化工园区危险态势感知

[J]. 化工学报, 2019, 70(2): 460-466.

Dou S, Zhang G Y, Xiong Z H, et al.

Danger situation awareness of chemical industry park based on multiple source data fusion

[J]. CIESC Journal, 2019, 70(2): 460-466.

袁亮, 俞啸, 丁恩杰, 等.

矿山物联网人-机-环状态感知关键技术研究

[J]. 通信学报, 2020, 41(2): 1-12.

Yuan L, Yu X, Ding E J, et al.

Research on key technologies of human-machine-environment states perception in mine Internet of Things

[J]. Journal on Communications, 2020, 41(2): 1-12.

侯慧, 于士文, 肖祥, 等.

基于空间多源异构数据的台风下输电杆塔风险评估

[J]. 电力系统自动化, 2020, 44(10): 127-134.

[本文引用: 1]

Hou H, Yu S W, Xiao X, et al.

Risk assessment of transmission tower in typhoon based on spatial multi-source heterogeneous data

[J]. Automation of Electric Power Systems, 2020, 44(10): 127-134.

[本文引用: 1]

何一帆.

基于多源异构数据融合的深度学习故障诊断

[D]. 开封: 河南大学, 2019.

[本文引用: 1]

He Y F.

Deep learning fault diagnosis based on multi-source heterogeneous data fusion

[D]. Kaifeng: Henan University, 2019.

[本文引用: 1]

孔岱, 李红伟.

模糊Petri网在压缩机故障诊断中的应用

[J]. 计算机工程与设计, 2018, 39(1): 271-275.

[本文引用: 2]

Kong D, Li H W.

Fuzzy Petri nets and its application in fault diagnosis of compressor

[J]. Computer Engineering and Design, 2018, 39(1): 271-275.

[本文引用: 2]

李娜, 孙文勇, 李佳宜.

保护层分析方法研究及其在风险分析中的应用

[J]. 石油与天然气化工, 2013, 42(6): 663-666.

[本文引用: 1]

Li N, Sun W Y, Li J Y.

Layers of Protection Analysis(LOPA)method and application of risk analysis

[J]. Chemical Engineering of Oil & Gas, 2013, 42(6): 663-666.

[本文引用: 1]

孙国豪, 鹿剑, 马斌良, 等.

石化装置静设备动态风险计算方法浅析

[J]. 中国特种设备安全, 2017, 33(4): 24-29.

[本文引用: 1]

Sun G H, Lu J, Ma B L, et al.

Discussion of dynamic risk assessment calculation method for petrochemical static equipment

[J]. China Special Equipment Safety, 2017, 33(4): 24-29.

[本文引用: 1]

刘俊芳.

石化行业人因可靠性分析及其在LOPA中的应用研究

[D]. 青岛: 中国石油大学(华东), 2015.

[本文引用: 1]

Liu J F.

Research on human reliability and its application in LOPA for petrochemical industry

[D]. Dongying, China: China University of Petroleum, 2015.

[本文引用: 1]

谢红卫, 孙志强, 李欣欣, 等.

典型人因可靠性分析方法评述

[J]. 国防科技大学学报, 2007, 29(2): 101-107.

[本文引用: 1]

Xie H W, Sun Z Q, Li X X, et al.

An overview of typical methods for human reliability analysis

[J]. Journal of National University of Defense Technology, 2007, 29(2): 101-107.

[本文引用: 1]

王洪德, 高玮.

基于人的认知可靠性(HCR)模型的人因操作失误研究

[J]. 中国安全科学学报, 2006, 16(7): 51-56.

[本文引用: 1]

Wang H D, Gao W.

Study on erroneous operation due to human factor based on human cognitive reliability(HCR) model

[J]. China Safety Science Journal (CSSJ), 2006, 16(7): 51-56.

[本文引用: 1]

王俊, 丁兰蓉.

安全完整性等级SIL的验证方法

[J]. 化工与医药工程, 2015, 36(2): 53-57.

[本文引用: 1]

Wang J, Ding L R.

Method of safety integrity level validation

[J]. Chemical and Pharmaceutical Engineering, 2015, 36(2): 53-57.

[本文引用: 1]

耿雪梅, 李宏光.

考虑人因指标的过程报警阈值自适应优化方法

[J]. 化工学报, 2018, 69: 95-101.

[本文引用: 1]

Geng X M, Li H G.

An adaptive optimization approach to process alarm thresholds concerning human factors

[J]. CIESC Journal, 2018, 69: 95-101.

[本文引用: 1]

袁雄军, 朱常龙, 葛秀坤, 等.

危险化学品泄漏事故点火概率取值研究

[J]. 中国安全科学学报, 2011, 21(9): 39-45.

[本文引用: 2]

Yuan X J, Zhu C L, Ge X K, et al.

Study on values taking of ignition probabilities in hazardous chemical leakage accidents

[J]. China Safety Science Journal, 2011, 21(9): 39-45.

[本文引用: 2]

Moosemiller M.

Development of algorithms for predicting ignition probabilities and explosion frequencies

[J]. Journal of Loss Prevention in the Process Industries, 2011, 24(3): 259-265.

[本文引用: 1]

/

〈 〉

版权所有 © 2019 《化工学报》编辑部
北京市东城区青年湖南街13号（100011）
电话：010-64519489，010-64519362，010-64519485，010-64519490，010-64519451
E-Mail：hgxb@cip.com.cn
京ICP备12046843号-7
京公网安备 11010102001995号
本系统由北京玛格泰克科技发展有限公司设计开发