磁性纳米流体颗粒定向排布与各向异性导热的数值模拟研究

doi:10.11949/0438-1157.20250414

摘要/Abstract

摘要：

磁性纳米流体因其独特的磁诱导定向排布特性与传热强化性能，在能源工程领域具有重要应用。利用格子Boltzmann方法（LBM）与离散单元法（DEM），建立了包括磁力的多作用力颗粒动力学模型。创新性地引入取向张量定量表征不同磁场下的颗粒链空间结构。结果表明，随着磁场强度的增大，颗粒沿磁场方向的定向排布程度逐渐提高。在200、500和1000 G的磁场强度下，磁场方向的取向张量分量分别为0.506、0.758及0.972。进一步采用热格子Boltzmann方法（T-LBM）模拟了磁场调控下的导热特性，揭示了取向张量通过表征颗粒链的空间构型来有效量化各向异性导热的机制。建立了考虑取向张量的热导率修正模型，该模型展示出了对磁诱导各向异性热导率良好的预测能力。

关键词: 磁性纳米流体, 颗粒聚集, 两相流, 数值模拟, 热传导

Abstract:

Magnetic nanofluids have significant applications in the field of energy engineering due to their unique magnetically induced orientation characteristics and enhanced heat transfer capabilities. A multi-force particle dynamics model, incorporating magnetic forces, was developed using the lattice Boltzmann method (LBM) coupled with the discrete element method (DEM). The orientation tensor was innovatively introduced to quantitatively characterize the spatial structure of particle chains under varying magnetic fields. The results show that the degree of particle alignment along the magnetic field direction increases with the strength of the applied field. Under magnetic field strengths of 200, 500, and 1000 G, the orientation tensor components in the magnetic field direction were 0.506, 0.758, and 0.972, respectively. Additionally, the thermal lattice Boltzmann method (T-LBM) was employed to simulate the thermal conductivity under magnetic field regulation. The mechanism by which the orientation tensor effectively quantifies anisotropic thermal conductivity through the characterization of the spatial configuration of particle chains was elucidated. A modified model incorporating the orientation tensor was proposed, demonstrating good predictive capability for magnetically induced anisotropic thermal conductivity.

Key words: magnetic nanofluids, particle aggregation, two-phase flow, numerical simulation, heat conduction

中图分类号:

TK 121

武顺杰, 蔡容容, Eliseev A.A., 张立志. 磁性纳米流体颗粒定向排布与各向异性导热的数值模拟研究[J]. 化工学报, DOI: 10.11949/0438-1157.20250414.

Shunjie WU, Rongrong CAI, A.A. Eliseev, Lizhi ZHANG. Numerical simulation study on particle orientation and anisotropic thermal conductivity in magnetic nanofluids[J]. CIESC Journal, DOI: 10.11949/0438-1157.20250414.

图/表 12

图1 边界条件示意图

Fig.1 Schematic of boundary conditions

表1 模拟参数

Table 1 Simulation parameters

模拟参数	数值	单位
颗粒密度， $ρ p$	5000	kg/m³
颗粒半径， $r p$	2.6×10^-8	m
Hamaker常数， $A H$	8.5×10^-20	J
颗粒体积分数，φ	1.0%	—
磁场强度，B	0-1000	G
流体密度， $ρ f$	1000	kg/m³
流体动力学粘度， $μ f$	0.001	kg/(m·s)
温度， $T$	335	K
计算域尺寸， $L 0$	3.22×10^-6	m
Zeta电势， $ψ 0$	-0.015	V

表1 模拟参数

Table 1 Simulation parameters

模拟参数	数值	单位
颗粒密度， $ρ p$	5000	kg/m³
颗粒半径， $r p$	2.6×10^-8	m
Hamaker常数， $A H$	8.5×10^-20	J
颗粒体积分数，φ	1.0%	—
磁场强度，B	0-1000	G
流体密度， $ρ f$	1000	kg/m³
流体动力学粘度， $μ f$	0.001	kg/(m·s)
温度， $T$	335	K
计算域尺寸， $L 0$	3.22×10^-6	m
Zeta电势， $ψ 0$	-0.015	V

表2 T-LBM模拟与Maxwell和Bruggeman模型的ETC结果比较

Table 2 Comparison of ETC results between T-LBM simulation and Maxwell and Bruggeman models

颗粒均匀分布的各工况纳米流体	颗粒体积分数或热导率比	有效热导率增强k_eff/k_f
颗粒均匀分布的各工况纳米流体	颗粒体积分数或热导率比	T-LBM	Maxwell	Bruggeman
不同颗粒体积分数的 SiO₂/甲醇纳米流体	0.1%	1.003	1.002	1.002
	0.5%	1.010	1.010	1.010
	1.0%	1.022	1.020	1.020
	2.0%	1.041	1.041	1.041
	5.0%	1.103	1.103	1.108
不同颗粒-基液热导率比的纳米流体	SiO₂/H₂O = 2.4 CuO/H₂O = 16.9 Fe₃O₄/kerosene = 76.9 Al₂O₃/methanol = 147.9 SiC/H₂O = 288.1	1.010	1.010	1.010
		1.030	1.025	1.026
		1.038	1.029	1.030
		1.039	1.030	1.030
		1.040	1.030	1.031

图2 T-LBM模型验证模拟图

Fig.2 Simulation schematic of T-LBM model validation

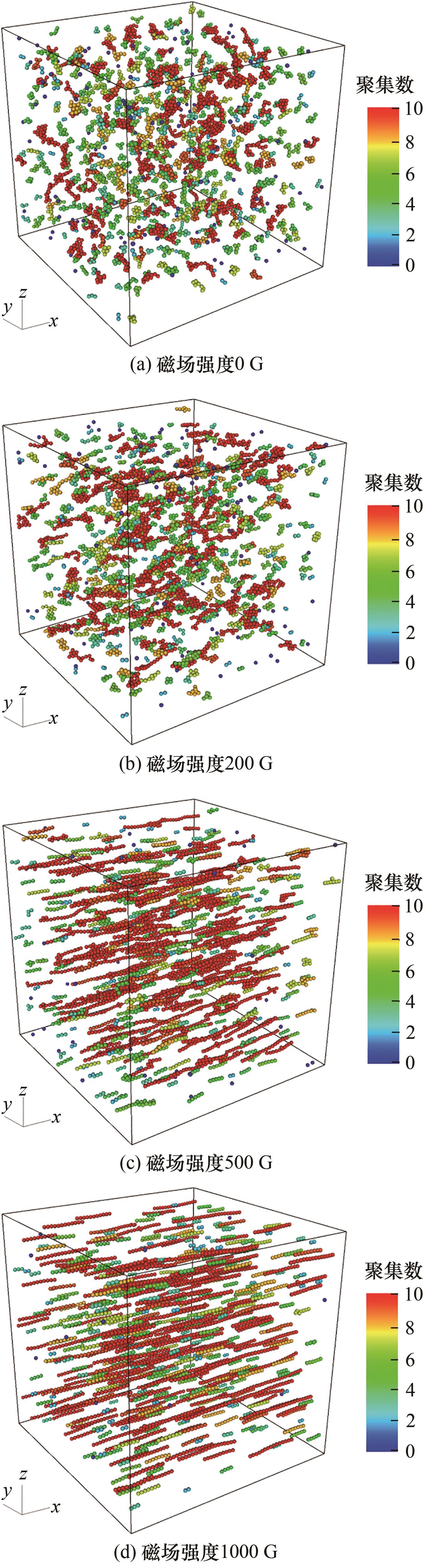
图3 不同磁场强度下的颗粒定向排布，聚集数为单链中的颗粒数量

Fig.3 Particle directional alignment under varying magnetic field intensities, with the aggregation number being the number of particles in a single chain

图4 聚集体取向张量的计算示意图

Fig.4 The schematic for calculating the orientation tension of aggregations

图5 不同磁场下的取向张量 T，内嵌图为典型聚集体结构

Fig.5 Orientation tensor T under varying magnetic fields, with the inset showing typical aggregation structures

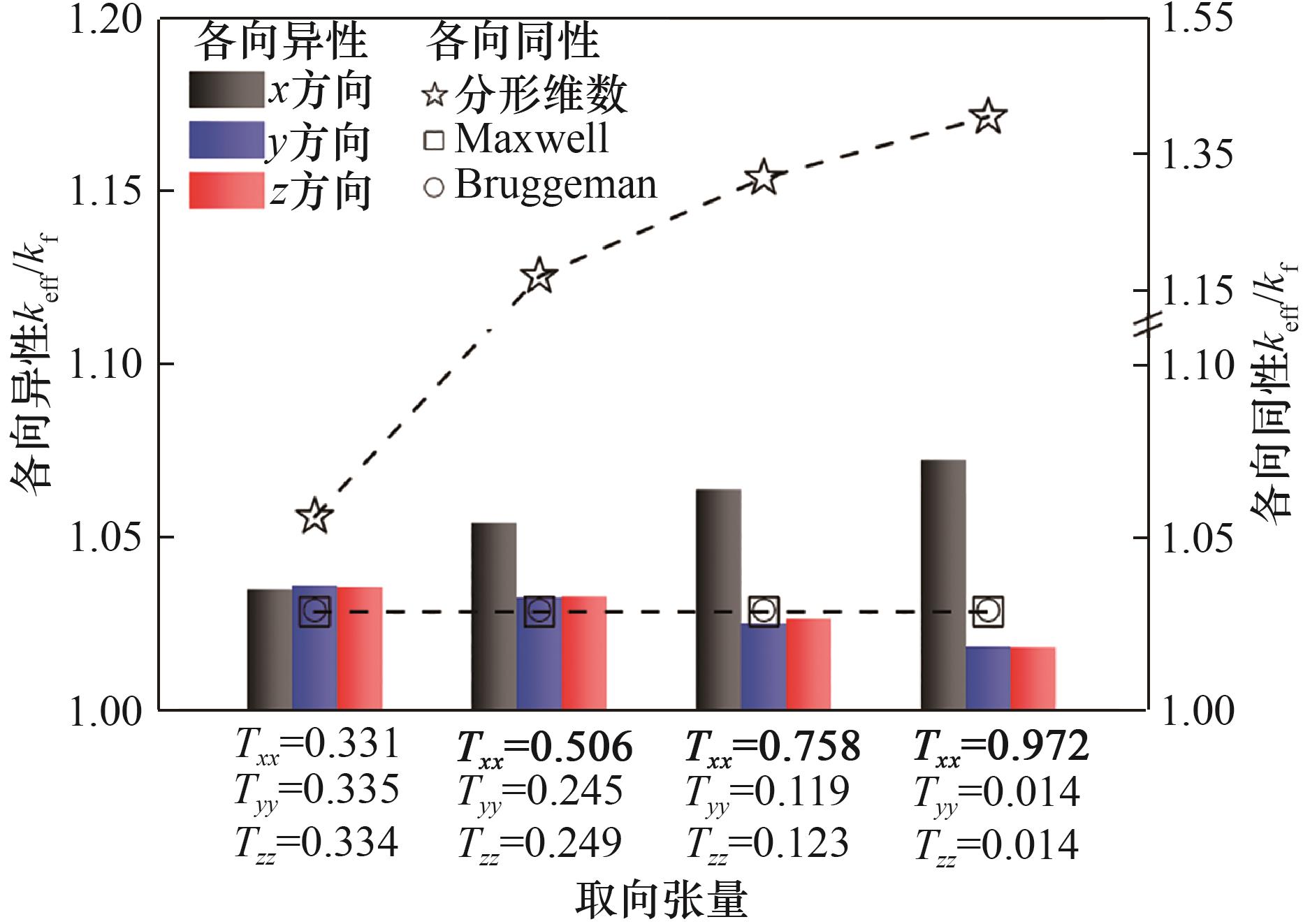
图6 不同取向张量下x、y、z方向ETC增强的模拟结果，以及与各向同性模型的对比

Fig.6 Simulation results of ETC enhancement in x, y and z directions under different orientation tensors, along with comparison to isotropic models

图7 取向张量 T 对聚集体各向导热的定量表征

Fig.7 Quantitative characterization for anisotropic heat conduction in aggregations using orientation tensor T

图8 回归模型的拟合性能，均方根误差为0.394%，决定系数R²为0.979

Fig.8 Fitting performance of the regression model, with a root mean square error of 0.394% and a coefficient of determination (R²) of 0.979

图9 磁性纳米流体keff/kf的模型预测与文献数据[8, 46]的对比

Fig.9 Comparison of model predictions of magnetic nanofluid keff/kf with reference data[8, 46]

图10 磁性纳米流体keff/kf的模型预测与实验数据的对比

Fig.10 Comparison of model predictions of magnetic nanofluid keff/kf with experimental data

参考文献 46

[1]	Aneke M, Wang M H. Energy storage technologies and real life applications–A state of the art review[J]. Applied Energy, 2016, 179: 350-377.
[2]	Lenin R, Joy P A, Bera C. A review of the recent progress on thermal conductivity of nanofluid[J]. Journal of Molecular Liquids, 2021, 338: 116929.
[3]	Malekan M, Khosravi A, Zhao X W. The influence of magnetic field on heat transfer of magnetic nanofluid in a double pipe heat exchanger proposed in a small-scale CAES system[J]. Applied Thermal Engineering, 2019, 146: 146-159.
[4]	Sheikhpour M, Arabi M, Kasaeian A, et al. Role of nanofluids in drug delivery and biomedical technology: methods and applications[J]. Nanotechnology, Science and Applications, 2020, 13: 47-59.
[5]	Qi C, Tang J H, Fan F, et al. Effects of magnetic field on thermo-hydraulic behaviors of magnetic nanofluids in CPU cooling system[J]. Applied Thermal Engineering, 2020, 179: 115717.
[6]	马连湘, 常强, 侯晓旭, 等. Fe₃O₄包覆碳纳米管磁流体制备及其在磁场中热导率的研究[J]. 功能材料, 2015, 46(24): 24114-24117.
	Ma L X, Chang Q, Hou X X, et al. The study of preparation and thermal conductivity of magnetic nanofluid based Fe₃O₄ coated on carbon nanotubes nanoparticles in amagnetic field[J]. Journal of Functional Materials, 2015, 46(24): 24114-24117.
[7]	Philip J, Shima P D, Raj B. Enhancement of thermal conductivity in magnetite based nanofluid due to chainlike structures[J]. Applied Physics Letters, 2007, 91(20): 203108.
[8]	Hajiyan M, Ebadi S, Mahmud S, et al. Experimental investigation of the effect of an external magnetic field on the thermal conductivity and viscosity of Fe₃O₄–glycerol[J]. Journal of Thermal Analysis and Calorimetry, 2019, 135(2): 1451-1464.
[9]	Katiyar A, Dhar P, Nandi T, et al. Enhanced heat conduction characteristics of Fe, Ni and Co nanofluids influenced by magnetic field[J]. Experimental Thermal and Fluid Science, 2016, 78: 345-353.
[10]	Zhang J F. Lattice Boltzmann method for microfluidics: models and applications[J]. Microfluidics and Nanofluidics, 2011, 10(1): 1-28.
[11]	Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47-65.
[12]	Liu H H, Surawanvijit S, Rallo R, et al. Analysis of nanoparticle agglomeration in aqueous suspensions via constant-number Monte Carlo simulation[J]. Environmental Science & Technology, 2011, 45(21): 9284-9292.
[13]	Chen Y J, Li Y Y, Liu Z H. Numerical simulations of forced convection heat transfer and flow characteristics of nanofluids in small tubes using two-phase models[J]. International Journal of Heat and Mass Transfer, 2014, 78: 993-1003.
[14]	Bahiraei M. A comprehensive review on different numerical approaches for simulation in nanofluids: traditional and novel techniques[J]. Journal of Dispersion Science and Technology, 2014, 35(7): 984-996.
[15]	Luding S. Introduction to discrete element methods[J]. European Journal of Environmental and Civil Engineering, 2008, 12(7/8): 785-826.
[16]	Noble D R, Torczynski J R. A lattice-Boltzmann method for partially saturated computational cells[J]. International Journal of Modern Physics C, 1998, 9(8): 1189-1201.
[17]	Fu S T, Su W T, Zhang H H, et al. An immersed moving boundary for fast discrete particle simulation with complex geometry[J]. Chemical Engineering Science, 2024, 283: 119407.
[18]	Li A, Ahmadi G. Dispersion and deposition of spherical particles from point sources in a turbulent channel flow[J]. Aerosol Science Technology, 1992, 16(4): 209-226.
[19]	Cunningham E. On the velocity of steady fall of spherical particles through fluid medium[J]. Proceedings of The Royal Society A-Mathematical Physical and Engineering Sciences, 1910, 83(563): 357-365.
[20]	Durhuus F L, Wandall L H, Boisen M H, et al. Simulated clustering dynamics of colloidal magnetic nanoparticles[J]. Nanoscale, 2021, 13(3): 1970-1981.
[21]	Agmo Hernández V. An overview of surface forces and the DLVO theory[J]. ChemTexts, 2023, 9(4): 10.
[22]	Hamaker H C. The London: van der Waals attraction between spherical particles[J]. Physica, 1937, 4(10): 1058-1072.
[23]	Ye Y, Cui A Y, Zhu L Q, et al. Electric-double-layer oriented field-screening effect on high-resolution electromechanical imaging in conductive solutions[J]. Physical Review Applied, 2019, 12(3): 034006.
[24]	Srinivasan S, Van den Akker H E A, Shardt O. Inclusion of DLVO forces in simulations of non-Brownian solid suspensions: Rheology and structure[J]. International Journal of Multiphase Flow, 2022, 149: 103929.
[25]	Karimnejad S, Delouei A A, Başağaoğlu H, et al. A review on contact and collision methods for multi-body hydrodynamic problems in complex flows[J]. Communications in Computational Physics, 2022, 32(4): 899-950.
[26]	Yang M M, Li S Q, Yao Q. Mechanistic studies of initial deposition of fine adhesive particles on a fiber using discrete-element methods[J]. Powder Technology, 2013, 248: 44-53.
[27]	Yue L Q, Chai Z H, Wang L, et al. A lattice Boltzmann model for the conjugate heat transfer[J]. International Journal of Heat and Mass Transfer, 2021, 165: 120682.
[28]	Li L K, Chen C, Mei R W, et al. Conjugate heat and mass transfer in the lattice Boltzmann equation method[J]. Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics, 2014, 89(4): 043308.
[29]	Tahmooressi H, Kasaeian A, Yavarinasab A, et al. Numerical simulation of nanoparticles size/aspect ratio effect on thermal conductivity of nanofluids using lattice Boltzmann method[J]. International Communications in Heat and Mass Transfer, 2021, 120: 105033.
[30]	Korba D, Wang N Q, Li L K. Accuracy of interface schemes for conjugate heat and mass transfer in the lattice Boltzmann method[J]. International Journal of Heat and Mass Transfer, 2020, 156: 119694.
[31]	阚安康, 康利云, 曹丹, 等. 基于Lattice-Boltzmann方法的纳米颗粒多孔介质导热特性[J]. 化工学报, 2015, 66(11): 4412-4417.
	Kan A K, Kang L Y, Cao D, et al. Thermal conduction characteristic of nano-granule porous material using lattice-Boltzmann method[J]. CIESC Journal, 2015, 66(11): 4412-4417.
[32]	Guo Z L, Zheng C G, Shi B C. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method[J]. Chinese Physics, 2002, 11(4): 366-374.
[33]	Gnedin N Y, Semenov V A, Kravtsov A V. Enforcing the Courant–Friedrichs–Lewy condition in explicitly conservative local time stepping schemes[J]. Journal of Computational Physics, 2018, 359: 93-105.
[34]	Zhang P, Galindo-Torres S A, Tang H W, et al. An efficient Discrete Element Lattice Boltzmann model for simulation of particle-fluid, particle-particle interactions[J]. Computers & Fluids, 2017, 147: 63-71.
[35]	Liu Z X, Zhu Y Z, Clausen J R, et al. Multiscale method based on coupled lattice-Boltzmann and Langevin-dynamics for direct simulation of nanoscale particle/polymer suspensions in complex flows[J]. International Journal for Numerical Methods in Fluids, 2019, 91(5): 228-246.
[36]	Fu S T, Wang L M. GPU-based unresolved LBM-DEM for fast simulation of gas–solid flows[J]. Chemical Engineering Journal, 2023, 465: 142898.
[37]	Maxwell J C. A Treatise on Electricity and Magnetism[M]. Cambridge, UK: Cambridge University Press, 2010.
[38]	Bruggeman D A G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen[J]. Annalen der Physik, 1935, 416(8): 665-679.
[39]	Barocas V H, Tranquillo R T. An anisotropic biphasic theory of tissue-equivalent mechanics: the interplay among cell traction, fibrillar network deformation, fibril alignment, and cell contact guidance[J]. Journal of Biomechanical Engineering, 1997, 119(2): 137-145.
[40]	Stylianopoulos T, Barocas V H. Multiscale, structure-based modeling for the elastic mechanical behavior of arterial walls[J]. Journal of Biomechanical Engineering, 2007, 129(4): 611-618.
[41]	Wei W, Cai J C, Hu X Y, et al. Fractal analysis of the effect of particle aggregation distribution on thermal conductivity of nanofluids[J]. Physics Letters A, 2016, 380(37): 2953-2956.
[42]	Evans W, Prasher R, Fish J, et al. Effect of aggregation and interfacial thermal resistance on thermal conductivity of nanocomposites and colloidal nanofluids[J]. International Journal of Heat and Mass Transfer, 2008, 51(5/6): 1431-1438.
[43]	Hamilton R L, Crosser O K. Thermal conductivity of heterogeneous two-component systems[J]. Industrial & Engineering Chemistry Fundamentals, 1962, 1(3): 187-191.
[44]	Yamada E, Ota T. Effective thermal conductivity of dispersed materials[J]. Wärme - und Stoffübertragung, 1980, 13(1): 27-37.
[45]	Fricke H. A mathematical treatment of the electric conductivity and capacity of disperse systems I. the electric conductivity of a suspension of homogeneous spheroids[J]. Physical Review, 1924, 24(5): 575-587.
[46]	Li Q, Xuan Y M, Wang J. Experimental investigations on transport properties of magnetic fluids[J]. Experimental Thermal and Fluid Science, 2005, 30(2): 109-116.