颗粒破碎的离散元及有限离散元模拟方法比较

doi:10.11949/0438-1157.20250078

摘要/Abstract

摘要：

颗粒物料团聚体在化工过程中普遍存在，其在运输时常因内部相互作用或与反应器碰撞引发变形及破碎现象。这些破坏过程时间极短，传统实验手段难以有效观测。离散元方法（DEM）和有限元方法（FEM）是两种常见的数值模拟方法。结合这两种方法的优势，有限离散元方法（FDEM）应运而生。使用改进的弹塑性铁摩辛柯梁胶结DEM模型（上交胶结模型，SJBM）与弹塑性FDEM模型，分别对颗粒碰撞和单轴压缩进行模拟。结果表明，SJBM能更精细刻画颗粒体系的应力集中与演化，在变形过程中展现出更细节的微观力学特征；FDEM在保证模拟精度的前提下，自动转换材料行为，具有相对较低的计算资源消耗。两种方法的比较，为更复杂化工过程优化和颗粒过程预测提供了模拟工具的选择依据。

关键词: 颗粒物料, 离散元方法, 有限离散元方法, 上交胶结模型, 颗粒过程, 数值模拟

Abstract:

Particle material agglomerates are common in chemical processes. They often cause deformation and crushing due to internal interactions or collisions with reactors during transportation. Since these destructive processes occur over extremely short time spans, traditional experimental methods struggle to achieve effective observation. Numerical simulation tools, such as the discrete element method (DEM) and the finite element method (FEM), provide effective means to reveal such transient processes. Leveraging the strengths of both approaches, the combined finite-discrete element method (FDEM) has been proposed and applied in related research. This study employs an improved elastoplastic Timoshenko beam-bonded DEM model (referred to as the Shanghai Jiaotong bond model, SJBM) and an elastoplastic FDEM model to comparatively simulate particle collision and uniaxial compression processes. The results demonstrate that the SJBM model can more precisely capture stress concentration and evolution characteristics within particle systems, particularly revealing richer micro-mechanical details during dynamic deformation processes. FDEM ensures simulation accuracy while automatically transitioning material behavior and maintaining relatively low computational resource consumption. The comparison between these two methods provides a basis for selecting model tools to optimize more complex chemical processes and particulate processes.

Key words: granular materials, discrete element method (DEM), finite-discrete element method (FDEM), Shanghai Jiaotong bond model (SJBM), particulate processes, numerical simulation

中图分类号:

TQ 021.5

杨开源, 陈锡忠. 颗粒破碎的离散元及有限离散元模拟方法比较[J]. 化工学报, 2025, 76(9): 4398-4411.

Kaiyuan YANG, Xizhong CHEN. Comparison of discrete element method and finite-discrete element method for simulation of agglomerate breakage[J]. CIESC Journal, 2025, 76(9): 4398-4411.

图/表 17

表1 非胶结接触的参数计算公式

Table 1 Formula for calculating parameters of non-bonded contact

变量	公式
法向力	$F n = F n s + F n d$
法向弹性力、法向阻尼力	$F n s = 43 E * R * δ n 1.5, F n d = - 256 η n S n m * u n, r$
切向力和其限制	$F t = F t s + F t d, F t, l i m i t = - μ s F n t a b$
切向弹性力、切向阻尼力	$F t s = - S t δ t, F t d = - 256 η t S t m * u t, r$
定向恒定扭矩	$T i = - μ r F n r i ω i$
法向重叠量、切向重叠量	$δ n = R a + R b - r b - r a, δ t = ∫ t c t u t, r d t, F t ≤ μ f F n μ f F n t a b k t, F t > μ f F n$
法向单位向量、切向单位向量	$n a b = r b - r a r b - r a, t a b = u r, t u r, t$
阻尼常数	$η n = η t = l n e π 2 + l n 2 e$
等效质量、等效半径	$m * = m a m b m a + m b, R * = R a R b R a + R b$
等效杨氏模量、等效剪切模量	$1 E * = 1 - ν a 2 E a + 1 - ν b 2 E b, 1 G * = 2 - ν a G a + 2 - ν b G b$
法向刚度、剪切刚度	$S n = 2 E * R * δ n, S t = 8 G * R * δ n$
相对速度	$u a b = u a - u b + R a ω a + R b ω b × n a b$
法向相对速度、切向相对速度	$u a b, n = u a b ⋅ n a b n a b, u r, t = u a b - u a b, n$

表1 非胶结接触的参数计算公式

Table 1 Formula for calculating parameters of non-bonded contact

变量	公式
法向力	$F n = F n s + F n d$
法向弹性力、法向阻尼力	$F n s = 43 E * R * δ n 1.5, F n d = - 256 η n S n m * u n, r$
切向力和其限制	$F t = F t s + F t d, F t, l i m i t = - μ s F n t a b$
切向弹性力、切向阻尼力	$F t s = - S t δ t, F t d = - 256 η t S t m * u t, r$
定向恒定扭矩	$T i = - μ r F n r i ω i$
法向重叠量、切向重叠量	$δ n = R a + R b - r b - r a, δ t = ∫ t c t u t, r d t, F t ≤ μ f F n μ f F n t a b k t, F t > μ f F n$
法向单位向量、切向单位向量	$n a b = r b - r a r b - r a, t a b = u r, t u r, t$
阻尼常数	$η n = η t = l n e π 2 + l n 2 e$
等效质量、等效半径	$m * = m a m b m a + m b, R * = R a R b R a + R b$
等效杨氏模量、等效剪切模量	$1 E * = 1 - ν a 2 E a + 1 - ν b 2 E b, 1 G * = 2 - ν a G a + 2 - ν b G b$
法向刚度、剪切刚度	$S n = 2 E * R * δ n, S t = 8 G * R * δ n$
相对速度	$u a b = u a - u b + R a ω a + R b ω b × n a b$
法向相对速度、切向相对速度	$u a b, n = u a b ⋅ n a b n a b, u r, t = u a b - u a b, n$

表2 胶结接触的参数计算公式

Table 2 Calculation formula of bonded contact parameters

变量	公式	变量	公式
胶结长度	$L B = r b - r a$	Timoshenko剪切系数	$Φ s = 20 R B 2 1 + ν B 3 L B 2$
胶结半径	$R B = λ ⋅ m i n R a, R b$	胶结压缩强度	$σ C = S C ζ C N + 1$
胶结横截面积	$A B = π R B 2$	胶结拉伸强度	$σ T = S T ζ T N + 1$
转动惯量	$I B = π R B 4 4$	胶结剪切强度	$σ s = S s ζ s N + 1$
法向应力	$σ n = σ t + σ b$	胶结塑性强度	$σ p = S p ζ p N + 1$
Von-Mises应力	$σ v M = σ n 2 + 3 τ 2$	塑性软化系数	$k p = σ p / σ v M$

表2 胶结接触的参数计算公式

Table 2 Calculation formula of bonded contact parameters

变量	公式	变量	公式
胶结长度	$L B = r b - r a$	Timoshenko剪切系数	$Φ s = 20 R B 2 1 + ν B 3 L B 2$
胶结半径	$R B = λ ⋅ m i n R a, R b$	胶结压缩强度	$σ C = S C ζ C N + 1$
胶结横截面积	$A B = π R B 2$	胶结拉伸强度	$σ T = S T ζ T N + 1$
转动惯量	$I B = π R B 4 4$	胶结剪切强度	$σ s = S s ζ s N + 1$
法向应力	$σ n = σ t + σ b$	胶结塑性强度	$σ p = S p ζ p N + 1$
Von-Mises应力	$σ v M = σ n 2 + 3 τ 2$	塑性软化系数	$k p = σ p / σ v M$

图1 SJBM中的接触示意图

Fig.1 Schematic diagram of contact in SJBM

表3 力和力矩增量计算的公式［34］

Table 3 Incremental forces and moments calculations［34］

变量定义	计算公式
轴向（法向）力	$Δ F a x = E B A B L B Δ u x Δ t$ $Δ F b x = - Δ F a x$
切向力	$Δ F a y = 12 E B I B L B 3 1 + Φ s Δ u y Δ t + 6 E B I B L B 2 1 + Φ s ω a z + ω b z Δ t$ $Δ F a z = 12 E B I B L B 3 1 + Φ s Δ u z Δ t + 6 E B I B L B 2 1 + Φ s ω a y + ω b y Δ t$ $Δ F b y = - Δ F a y$ $Δ F b z = - Δ F a z$
扭转力矩	$Δ M a x = E B L B 1 + ν B I B Δ ω x Δ t$ $Δ M b x = - Δ M a x$
弯曲力矩	$Δ M a y = - 6 E B I B L B 2 1 + Φ s Δ u z Δ t + E B I B 4 + Φ s L B 1 + Φ s Δ ω a y Δ t + E B I B 2 - Φ s L B 1 + Φ s Δ ω b y Δ t$ $Δ M a z = 6 E B I B L B 2 1 + Φ s Δ u y Δ t + E B I B 4 + Φ s L B 1 + Φ s Δ ω a z Δ t + E B I B 2 - Φ s L B 1 + Φ s Δ ω b z Δ t$ $Δ M b y = - 6 E B I B L B 2 1 + Φ s Δ u z Δ t + E B I B 4 + Φ s L B 1 + Φ s Δ ω b y Δ t + E B I B 2 - Φ s L B 1 + Φ s Δ ω a y Δ t$ $Δ M b z = 6 E B I B L B 2 1 + Φ s Δ u y Δ t + E B I B 4 + Φ s L B 1 + Φ s Δ ω b z Δ t + E B I B 2 - Φ s L B 1 + Φ s Δ ω a z Δ t$

表3 力和力矩增量计算的公式［34］

Table 3 Incremental forces and moments calculations［34］

变量定义	计算公式
轴向（法向）力	$Δ F a x = E B A B L B Δ u x Δ t$ $Δ F b x = - Δ F a x$
切向力	$Δ F a y = 12 E B I B L B 3 1 + Φ s Δ u y Δ t + 6 E B I B L B 2 1 + Φ s ω a z + ω b z Δ t$ $Δ F a z = 12 E B I B L B 3 1 + Φ s Δ u z Δ t + 6 E B I B L B 2 1 + Φ s ω a y + ω b y Δ t$ $Δ F b y = - Δ F a y$ $Δ F b z = - Δ F a z$
扭转力矩	$Δ M a x = E B L B 1 + ν B I B Δ ω x Δ t$ $Δ M b x = - Δ M a x$
弯曲力矩	$Δ M a y = - 6 E B I B L B 2 1 + Φ s Δ u z Δ t + E B I B 4 + Φ s L B 1 + Φ s Δ ω a y Δ t + E B I B 2 - Φ s L B 1 + Φ s Δ ω b y Δ t$ $Δ M a z = 6 E B I B L B 2 1 + Φ s Δ u y Δ t + E B I B 4 + Φ s L B 1 + Φ s Δ ω a z Δ t + E B I B 2 - Φ s L B 1 + Φ s Δ ω b z Δ t$ $Δ M b y = - 6 E B I B L B 2 1 + Φ s Δ u z Δ t + E B I B 4 + Φ s L B 1 + Φ s Δ ω b y Δ t + E B I B 2 - Φ s L B 1 + Φ s Δ ω a y Δ t$ $Δ M b z = 6 E B I B L B 2 1 + Φ s Δ u y Δ t + E B I B 4 + Φ s L B 1 + Φ s Δ ω b z Δ t + E B I B 2 - Φ s L B 1 + Φ s Δ ω a z Δ t$

图2 FDEM中两种网格单元的示意图

Fig.2 Schematic diagram of two types of mesh elements in FDEM

表4 弹塑性FDEM相关参数计算公式［28］

Table 4 Parameters calculations in the elastoplastic FDEM［28］

子模型	定义或说明	公式
弹塑性模型	应力平衡方程	$F e x = v a r - p t a n β - d = 0$ $v a r = 12 q 1 + 1 K - 1 - 1 K ε Ⅲ q 3$
	弹塑性内聚强度	$d = 1 + 13 t a n β σ t$
	拉伸屈服应力	$ε t = φ 1 - φ × F a d d b 2$
内聚裂缝模型	牵引分离模型的应力分量	$t r = 1 - D t r ¯$
	破坏率变量	$D = 1 - (δ 0 δ m a x) 1 - 1 - e x p - α δ m a x - δ 0 δ f - δ 0 1 - e x p - α$
	VE界面刚度	$k n = 10 E V E I e, k t = 10 G V E I e = 10 E V E 2 I e 1 + ν$
	CIE切向强度	$ε t a n = p ¯ t a n ϕ i + c, p ¯ = 13 σ x x + σ y y + σ z z$
	Mohr-Coulomb内聚强度	$c = σ t a n 2 1 - s i n ϕ i c o s ϕ i 1 K + 13 t a n β 1 - 13 t a n β, s i n ϕ i = 3 t a n β 6 + t a n β$
	主断裂能分量	$G I c = ∫ 0 δ n f t r n δ n d δ n, G Ⅱ c = G Ⅲ c = 5 G Ⅰ c$
	主断裂能	$G c = G Ⅰ c + G Ⅱ c - G Ⅰ c G s h e a r G T η$
	剪切断裂能、拉伸断裂能	$G s h e a r = G Ⅱ c + G Ⅲ c, G T = G Ⅰ c + G s h e a r$
	二次失效准则	$t r Ⅰ t r Ⅰ 0 2 + t r Ⅱ t r Ⅱ 0 2 + t r Ⅲ t r Ⅲ 0 2 = 1$ ，上角标0表示峰值
接触模型	接触阻尼力	$F v d = - μ 4 m n o d e k c v r e l$

表4 弹塑性FDEM相关参数计算公式［28］

Table 4 Parameters calculations in the elastoplastic FDEM［28］

子模型	定义或说明	公式
弹塑性模型	应力平衡方程	$F e x = v a r - p t a n β - d = 0$ $v a r = 12 q 1 + 1 K - 1 - 1 K ε Ⅲ q 3$
	弹塑性内聚强度	$d = 1 + 13 t a n β σ t$
	拉伸屈服应力	$ε t = φ 1 - φ × F a d d b 2$
内聚裂缝模型	牵引分离模型的应力分量	$t r = 1 - D t r ¯$
	破坏率变量	$D = 1 - (δ 0 δ m a x) 1 - 1 - e x p - α δ m a x - δ 0 δ f - δ 0 1 - e x p - α$
	VE界面刚度	$k n = 10 E V E I e, k t = 10 G V E I e = 10 E V E 2 I e 1 + ν$
	CIE切向强度	$ε t a n = p ¯ t a n ϕ i + c, p ¯ = 13 σ x x + σ y y + σ z z$
	Mohr-Coulomb内聚强度	$c = σ t a n 2 1 - s i n ϕ i c o s ϕ i 1 K + 13 t a n β 1 - 13 t a n β, s i n ϕ i = 3 t a n β 6 + t a n β$
	主断裂能分量	$G I c = ∫ 0 δ n f t r n δ n d δ n, G Ⅱ c = G Ⅲ c = 5 G Ⅰ c$
	主断裂能	$G c = G Ⅰ c + G Ⅱ c - G Ⅰ c G s h e a r G T η$
	剪切断裂能、拉伸断裂能	$G s h e a r = G Ⅱ c + G Ⅲ c, G T = G Ⅰ c + G s h e a r$
	二次失效准则	$t r Ⅰ t r Ⅰ 0 2 + t r Ⅱ t r Ⅱ 0 2 + t r Ⅲ t r Ⅲ 0 2 = 1$ ，上角标0表示峰值
接触模型	接触阻尼力	$F v d = - μ 4 m n o d e k c v r e l$

表5 SJBM模型的相关参数

Table 5 Parameters of the SJBM

变量及其描述	数值	变量及其描述	数值
团聚体颗粒直径d₀/mm	1.70	装置密度 $ρ r i g i d$ /(kg/m³)	7850
基础粒子总数量	12065	装置杨氏模量E_rigid/GPa	2000
胶结总数量	50258	装置泊松比 $ν r i g i d$	0.2
接触总数量	100516	基础粒子-装置间恢复系数e	0.5
全局阻尼 $η$	0	基础粒子-装置间静摩擦因数 $μ s$	0.16
胶结生成时间 $t B$ /s	1.0×10^-12	基础粒子-装置间滚动摩擦因数 $μ r$	0
最大基础粒子半径R_max/mm	0.00615	胶结杨氏模量E_B/GPa	162
最小基础粒子半径R_min/mm	0.0012	胶结泊松比 $ν$ _B	0.3
接触半径系数 $θ$	1.2	平均胶结压缩强度 $S C$ /MPa	1200
空隙率 $ε$	0.33	平均胶结拉伸强度 $S T$ /MPa	245
基础粒子密度 $ρ$ /(kg/m³)	3370	平均胶结剪切强度 $S s$ /MPa	115
基础粒子杨氏模量E/GPa	250	平均胶结塑性强度 $S p$ /MPa	用户自定
基础粒子泊松比 $ν$	0.2	胶结压缩、拉伸、剪切、塑性强度的变异系数 $ζ C, ζ T, ζ s, ζ p$	0
胶结半径系数 $λ$	1.1

表5 SJBM模型的相关参数

Table 5 Parameters of the SJBM

变量及其描述	数值	变量及其描述	数值
团聚体颗粒直径d₀/mm	1.70	装置密度 $ρ r i g i d$ /(kg/m³)	7850
基础粒子总数量	12065	装置杨氏模量E_rigid/GPa	2000
胶结总数量	50258	装置泊松比 $ν r i g i d$	0.2
接触总数量	100516	基础粒子-装置间恢复系数e	0.5
全局阻尼 $η$	0	基础粒子-装置间静摩擦因数 $μ s$	0.16
胶结生成时间 $t B$ /s	1.0×10^-12	基础粒子-装置间滚动摩擦因数 $μ r$	0
最大基础粒子半径R_max/mm	0.00615	胶结杨氏模量E_B/GPa	162
最小基础粒子半径R_min/mm	0.0012	胶结泊松比 $ν$ _B	0.3
接触半径系数 $θ$	1.2	平均胶结压缩强度 $S C$ /MPa	1200
空隙率 $ε$	0.33	平均胶结拉伸强度 $S T$ /MPa	245
基础粒子密度 $ρ$ /(kg/m³)	3370	平均胶结剪切强度 $S s$ /MPa	115
基础粒子杨氏模量E/GPa	250	平均胶结塑性强度 $S p$ /MPa	用户自定
基础粒子泊松比 $ν$	0.2	胶结压缩、拉伸、剪切、塑性强度的变异系数 $ζ C, ζ T, ζ s, ζ p$	0
胶结半径系数 $λ$	1.1

表6 弹塑性FDEM的相关参数

Table 6 Parameters of the elastoplastic FDEM

变量及其描述	数值	变量及其描述	数值
碰撞算例、单轴压缩算例单元数	40894，39784	剪切强度 $σ s$ /MPa	63
总体堆积密度 $ρ b u l k$ /mm³	1.04×10^-9	切向、法向界面刚度 $k t, k n$ /(N/mm)	4.00×10⁵, 1.54×10⁵
总体杨氏模量E_FDEM/MPa	4000	主应力分量 $t Ⅰ, t Ⅱ, t Ⅲ$ /MPa	16, 8, 8
总体泊松比 $ν$ _FDEM	0.3	切向、法向牵引模量 $E t, E n$ /MPa	2800, 1076.92
摩擦角 $β$	46.4	断裂能密度分量 $G Ⅰ c, G Ⅱ c, G Ⅲ c$ /(mJ/mm²)	0.00056, 0.0028, 0.0028
三轴实验拉伸压缩应力比率 $K$	0.778	团聚体直径 $d s$ /mm	1.7

表6 弹塑性FDEM的相关参数

Table 6 Parameters of the elastoplastic FDEM

变量及其描述	数值	变量及其描述	数值
碰撞算例、单轴压缩算例单元数	40894，39784	剪切强度 $σ s$ /MPa	63
总体堆积密度 $ρ b u l k$ /mm³	1.04×10^-9	切向、法向界面刚度 $k t, k n$ /(N/mm)	4.00×10⁵, 1.54×10⁵
总体杨氏模量E_FDEM/MPa	4000	主应力分量 $t Ⅰ, t Ⅱ, t Ⅲ$ /MPa	16, 8, 8
总体泊松比 $ν$ _FDEM	0.3	切向、法向牵引模量 $E t, E n$ /MPa	2800, 1076.92
摩擦角 $β$	46.4	断裂能密度分量 $G Ⅰ c, G Ⅱ c, G Ⅲ c$ /(mJ/mm²)	0.00056, 0.0028, 0.0028
三轴实验拉伸压缩应力比率 $K$	0.778	团聚体直径 $d s$ /mm	1.7

图3 碰撞结果示意图（从左到右：FDEM、SJBM和Antonyuk实验[6]）

Fig.3 Schematic diagrams of collision results (from left to right: FDEM, SJBM and Antonyuk’s experiment [6])

图4 SJBM和FDEM的碰撞力随时间变化曲线

Fig.4 Collision force via time curves of SJBM and FDEM

图5 SJBM和FDEM的颗粒归一化动能随时间变化曲线

Fig.5 Agglomerate’s normalized kinetic energy via time curves of SJBM and FDEM

图6 FDEM和SJBM中几个典型时刻的屈服应力云图

Fig.6 Yield stress contours at several typical timepoints in FDEM and SJBM

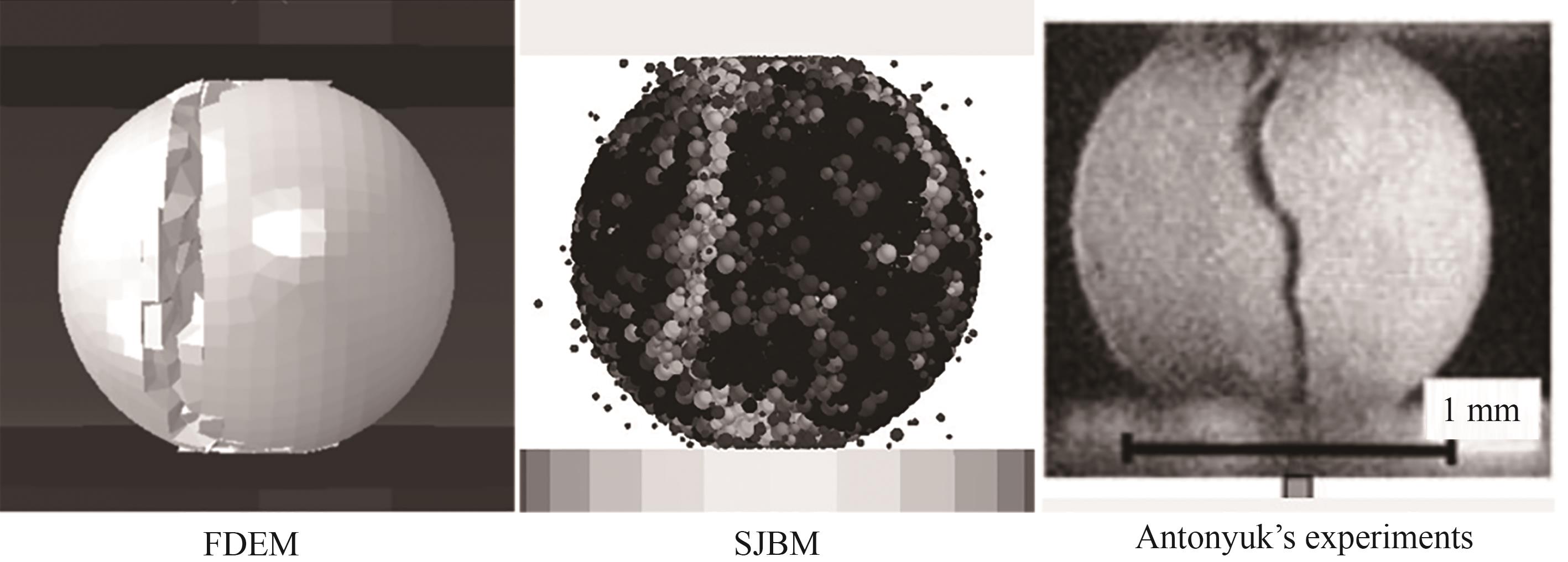
图7 单轴压缩结果示意图（从左到右：FDEM、SJBM和Antonyuk实验[10]）

Fig.7 Schematic diagrams of uniaxial compression results (from left to right: FDEM, SJBM and Antonyuk’s experiment [10])

图8 SJBM、FDEM和Antonyuk[10]的实验的压缩力随压缩位移变化曲线

Fig.8 Compression force-displacement curves of SJBM, FDEM and Antonyuk’s experiments[10]

图9 SJBM和FDEM的颗粒归一化动能随压缩位移变化曲线

Fig.9 Agglomerate’s normalized kinetic energy via compression-displacement curves of SJBM and FDEM

图10 FDEM和SJBM中几个典型位移的屈服应力云图

Fig.10 Yield stress contours at several typical displacements in FDEM and SJBM

表7 DEM和FDEM的特点比较

Table 7 Comparison of characteristics between DEM and FDEM

对比维度	离散元方法（DEM）	有限离散元方法（FDEM）
基本原理	基于离散基础粒子间的相互作用，通过牛顿运动方程更新基础粒子运动轨迹，模拟弹塑性变形和断裂行为	结合离散元（接触力计算）与有限元（连续域应力计算），实现材料从连续到不连续行为的自动转换
接触力计算	直接计算基础粒子间的接触力（如Hertz-Mindlin模型或胶结模型）	离散单元间计算接触力，连续域内通过有限元法计算内部应力
颗粒破碎机制	基于断裂准则（如Von-Mises屈服准则），通过局部应力判断接触破坏	采用内聚裂缝模型（ICZM），通过局部应力准则触发裂纹生成，并生成新的接触面
计算资源消耗	相对较高（需处理大量基础粒子动态变化、基础粒子接触及胶结动态更新）	相对适中（有限元网格分割减少接触计算量，但需额外处理黏性界面单元）
输入参数类型	基础粒子属性（如半径、密度、杨氏模量）及胶结参数（强度、变异系数）	材料属性（如杨氏模量、断裂能）和理论计算参数（如界面刚度、破坏率变量）
模拟精度与细节	更精细捕捉微观力学细节（如应力集中、“二次断裂”现象），适合复杂破裂模式分析	能模拟裂纹扩展及碎片生成，在保持精度的同时计算效率更高，适合大规模动态断裂场景
能量耗散特性	因空隙率和基础粒子间相对运动导致更高能量耗散（如碰撞案例中动能损失率更高）	能量耗散主要由连续域断裂和接触阻尼决定，耗散速度更快（如单轴压缩中压缩力下降更迅速）
适用场景	需高精度微观力学分析的场景（如颗粒局部断裂、动态应力演化）	需兼顾效率与精度的场景（如多裂纹扩展、材料行为自动转换）

表7 DEM和FDEM的特点比较

Table 7 Comparison of characteristics between DEM and FDEM

对比维度	离散元方法（DEM）	有限离散元方法（FDEM）
基本原理	基于离散基础粒子间的相互作用，通过牛顿运动方程更新基础粒子运动轨迹，模拟弹塑性变形和断裂行为	结合离散元（接触力计算）与有限元（连续域应力计算），实现材料从连续到不连续行为的自动转换
接触力计算	直接计算基础粒子间的接触力（如Hertz-Mindlin模型或胶结模型）	离散单元间计算接触力，连续域内通过有限元法计算内部应力
颗粒破碎机制	基于断裂准则（如Von-Mises屈服准则），通过局部应力判断接触破坏	采用内聚裂缝模型（ICZM），通过局部应力准则触发裂纹生成，并生成新的接触面
计算资源消耗	相对较高（需处理大量基础粒子动态变化、基础粒子接触及胶结动态更新）	相对适中（有限元网格分割减少接触计算量，但需额外处理黏性界面单元）
输入参数类型	基础粒子属性（如半径、密度、杨氏模量）及胶结参数（强度、变异系数）	材料属性（如杨氏模量、断裂能）和理论计算参数（如界面刚度、破坏率变量）
模拟精度与细节	更精细捕捉微观力学细节（如应力集中、“二次断裂”现象），适合复杂破裂模式分析	能模拟裂纹扩展及碎片生成，在保持精度的同时计算效率更高，适合大规模动态断裂场景
能量耗散特性	因空隙率和基础粒子间相对运动导致更高能量耗散（如碰撞案例中动能损失率更高）	能量耗散主要由连续域断裂和接触阻尼决定，耗散速度更快（如单轴压缩中压缩力下降更迅速）
适用场景	需高精度微观力学分析的场景（如颗粒局部断裂、动态应力演化）	需兼顾效率与精度的场景（如多裂纹扩展、材料行为自动转换）

参考文献 42

[1]	Thornton C, Liu L F. How do agglomerates break?[J]. Powder Technology, 2004, 143/144: 110-116.
[2]	Lai J Q, Wu C B, Liao N N, et al. A study on the correlation between fractal dimension and particle breakage for tungsten ores under impact crushing[J]. Minerals Engineering, 2024, 218: 108980.
[3]	Lowe A, Singh G, Chan H K, et al. Fragmentation dynamics of single agglomerate-to-wall impaction[J]. Powder Technology, 2021, 378: 561-575.
[4]	Han Y L, Zhao D, Chu Y H, et al. Breakage behaviour of single rice particles under compression and impact[J]. Advanced Powder Technology, 2021, 32(12): 4635-4650.
[5]	Kesanapalli C, Kang H. Elastic mode expansion in smoothed particle hydrodynamics framework for hydroelasticity and validation with 3D hydroelastic wedge impact experiments[J]. Marine Structures, 2025, 99: 103721.
[6]	Antonyuk S, Khanal M, Tomas J, et al. Impact breakage of spherical granules: experimental study and DEM simulation[J]. Chemical Engineering and Processing: Process Intensification, 2006, 45(10): 838-856.
[7]	Parab N D, Guo Z R, Hudspeth M C, et al. Fracture mechanisms of glass particles under dynamic compression[J]. International Journal of Impact Engineering, 2017, 106: 146-154.
[8]	Hermsmeyer S, Reimann J. Particle flow of ceramic breeder pebble beds in bi-axial compression experiments[J]. Fusion Engineering and Design, 2002, 61/62: 367-373.
[9]	Sheng Y, Briscoe B J, Maung R, et al. Compression of polymer bound alumina agglomerates at the micro deformation scale[J]. Powder Technology, 2004, 140(3): 228-239.
[10]	Antonyuk S, Tomas J, Heinrich S, et al. Breakage behaviour of spherical granulates by compression[J]. Chemical Engineering Science, 2005, 60(14): 4031-4044.
[11]	Potapov A V, Campbell C S. Computer simulation of impact-induced particle breakage[J]. Powder Technology, 1994, 81(3): 207-216.
[12]	Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979, 29(1): 47-65.
[13]	Clough R W. The finite element method in plane stress analysis[C]//2nd Conference on Electronic Computation. American Society of Civil Engineers, 1960: 345-378.
[14]	Tahmasebi P. A state-of-the-art review of experimental and computational studies of granular materials: properties, advances, challenges, and future directions[J]. Progress in Materials Science, 2023, 138: 101157.
[15]	Aleshin V, Van Den Abeele K. Preisach analysis of the hertz-mindlin system[J]. Journal of the Mechanics and Physics of Solids, 2009, 57(4): 657-672.
[16]	Mindlin R D, Deresiewicz H. Elastic spheres in contact under varying oblique forces[J]. Journal of Applied Mechanics, 1953, 20(3): 327-344.
[17]	Nguyen N H T, Bui H H, Nguyen G D, et al. A cohesive damage-plasticity model for DEM and its application for numerical investigation of soft rock fracture properties[J]. International Journal of Plasticity, 2017, 98: 175-196.
[18]	Liakas S, O'Sullivan C, Saroglou C. Influence of heterogeneity on rock strength and stiffness using discrete element method and parallel bond model[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017, 9(4): 575-584.
[19]	Xue C, Ye J X, Kuzuno R, et al. Fractional-order modelling and dynamic analysis on a typical beam structure incorporated with a semi-active particle damping equipment[J]. Powder Technology, 2024, 433: 119219.
[20]	Chen X Z, Peng D, Morrissey J P, et al. A comparative assessment and unification of bond models in DEM simulations[J]. Granular Matter, 2021, 24(1): 29.
[21]	Brown N J, Chen J F, Ooi J Y. A bond model for DEM simulation of cementitious materials and deformable structures[J]. Granular Matter, 2014, 16(3): 299-311.
[22]	Chen X Z, Wang L G, Morrissey J P, et al. DEM simulations of agglomerates impact breakage using Timoshenko beam bond model[J]. Granular Matter, 2022, 24(3): 74.
[23]	Wang L G, Ge R H, Chen X Z. Establishing an oblique impact breakage master curve using a DEM bonded contact model[J]. Computers and Geotechnics, 2022, 145: 104668.
[24]	Wang L, Yue C X, Liu X L, et al. Conventional and micro scale finite element modeling for metal cutting process: a review[J]. Chinese Journal of Aeronautics, 2024, 37(2): 199-232.
[25]	Kweon H D, Kim J W, Song O, et al. Determination of true stress-strain curve of type 304 and 316 stainless steels using a typical tensile test and finite element analysis[J]. Nuclear Engineering and Technology, 2021, 53(2): 647-656.
[26]	Tao J B, Zhang R, Guo R. Numerical analysis of particle reinforced composites with interphases by three-dimensional thermal-elasto-plastic Voronoi cell finite element method[J]. Composite Structures, 2025, 354: 118774.
[27]	Munjiza A, Rougier E, Knight E E, et al. Discrete and combined finite discrete element methods for computational mechanics of discontinua[M]//Comprehensive Structural Integrity. Amsterdam: Elsevier, 2023: 408-428.
[28]	Zhang Z Y, Liu D Y. A finite-discrete element model for simulating collision and fragmentation of nanoparticle agglomerates[J]. AIChE Journal, 2024, 70(1): e18275.
[29]	Zhou B, Wei D H, Ku Q, et al. Study on the effect of particle morphology on single particle breakage using a combined finite-discrete element method[J]. Computers and Geotechnics, 2020, 122: 103532.
[30]	Li Z F, Zhang Y F, Chen R, et al. Numerical investigation of morphological effects on crushing characteristics of single calcareous sand particle by finite-discrete element method[J]. Powder Technology, 2025, 453: 120592.
[31]	Brown N J. Discrete Element Modelling of Cementitious Materials[M]. Belfast: The University of Edinburgh, 2013: 247.
[32]	Brown N J, Morrissey J P, Ooi J Y, et al. EDEM Contact Model: Timoshenko Beam Bond Model[M]. Belfast: University of Edinburgh, Queen's University, 2015: 34.
[33]	Ali Faghidian S, Elishakoff I. The tale of shear coefficients in Timoshenko-Ehrenfest beam theory: 130 years of progress[J]. Meccanica, 2023, 58(1): 97-108.
[34]	Yang K Y, Liu C B, Hong K, et al. An elastoplastic beam bond model for DEM simulation of deformable materials and breakage behaviors[J]. AIChE Journal, 2025, 71(2): e18624.
[35]	Nguyen V D X, Tieu A K, André D, et al. Discrete element method using cohesive plastic beam for modeling elasto-plastic deformation of ductile materials[J]. Computational Particle Mechanics, 2021, 8(3): 437-457.
[36]	André D, Iordanoff I, Charles J L, et al. Discrete element method to simulate continuous material by using the cohesive beam model[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 213/214/215/216: 113-125.
[37]	Cornec A, Lilleodden E. Numerical analysis of micropillar compression behaviour and stress-strain curve estimation verified on glass fused silica[J]. Materials Today Communications, 2022, 33: 104971.
[38]	Koutous A, Hilali E. Compression stress-strain curve of rammed earth: measuring and modelling[J]. Results in Engineering, 2023, 18: 101012.
[39]	Zhao Y H, Guo Y Z, Wei Q, et al. Influence of specimen dimensions and strain measurement methods on tensile stress-strain curves[J]. Materials Science and Engineering: A, 2009, 525(1/2): 68-77.
[40]	Peng D, Wang L G, Lin Y Q, et al. Oblique impact breakage unification of nonspherical particles using discrete element method[J]. Particuology, 2024, 90: 61-71.
[41]	Guo Y, Wassgren C, Curtis J S, et al. A bonded sphero-cylinder model for the discrete element simulation of elasto-plastic fibers[J]. Chemical Engineering Science, 2018, 175: 118-129.
[42]	Chen X Z, Wang L G, Meng F L, et al. Physics-informed deep learning for modelling particle aggregation and breakage processes[J]. Chemical Engineering Journal, 2021, 426: 131220.