基于稳定性的循环物流系统流程模拟——以催化裂化反应-再生系统为例

doi:10.11949/0438-1157.20211472

摘要/Abstract

摘要：

过程流程模拟中广泛应用的序贯模块法处理循环物流系统存在很多困难，如断裂流股的选择、迭代方程的收敛性等。基于稳定性理论解决循环物流系统的流程模拟问题，首先根据化工单元装置的模型方程将其分为正向模型和反向模型，并将循环物流中的变量定义为迭代变量和收敛变量；然后在收敛变量处将循环物流的流股断裂，迭代变量分别通过正向模型和反向模型计算收敛变量，二者的偏差通过增益系数对迭代变量进行修正，进而得到迭代方程；最后，利用控制理论中的稳定性理论来确定迭代方程的增益系数，将迭代方程线性化，采用劳斯判据确定增益系数的稳定范围，当增益系数位于稳定范围以内时，迭代方程必然收敛。催化裂化装置反应-再生系统因催化剂循环的存在而成为典型的循环物流系统，本文将反应器作为正向模型，再生器作为反向模型，以再生温度和再生催化剂含碳量作为迭代变量，构造了催化裂化装置反应-再生系统流程模拟的迭代方程，利用稳定性理论找到增益系数的稳定范围，保证流程模拟计算必定达到收敛，验证了该方法的可行性和有效性。

关键词: 循环物流, 过程系统, 流程模拟, 催化裂化装置, 稳定性

Abstract:

The sequential modular method, which is widely used in process simulation, has many difficulties in dealing with stream circulation system, such as the selection of tearing stream and the convergence of iterative equations. Based on the stability theory, this paper solves the process simulation problem of stream circulation system. First, according to the model equation, chemical plants are identified as forward model and backward model, and the variables in stream circulation are defined as iterative variables and convergence variables respectively. Then, the stream circulation is broken at the convergence variables, and the convergence variables are calculated from the iterative variables by the forward model and the backward model respectively; the convergence errors are used for the correction of iterative variables through the gain coefficients, and then the iterative equation is obtained. Finally, the stability theory in control theory is used to determine the gain coefficient of the iterative equation, the iterative equation is linearized, and the Routh criterion is used to determine the stable range of the gain coefficient; when the gain coefficients is within the stable range, the iterative equation must converge. The reaction and regeneration system of FCCU is a typical stream circulation system because of catalyst circulation. The reactor is treated as the forward model and the regenerator is treated as the backward model. The temperature and carbon content of regenerator are treated as iteration variables to build the iterative equation of process simulation for FCCU reaction and regeneration system. The stability range of the gain coefficients is found by using the stability theory to ensure the convergence of the simulation calculation, and the feasibility and effectiveness of this method are verified.

Key words: stream circulation, process system, process simulation, FCCU, stability

中图分类号:

TQ 021.8

曹森山, 许锋, 罗雄麟. 基于稳定性的循环物流系统流程模拟——以催化裂化反应-再生系统为例[J]. 化工学报, 2022, 73(3): 1256-1269.

Senshan CAO, Feng XU, Xionglin LUO. Process simulation of stream circulation system based on stability:[J]. CIESC Journal, 2022, 73(3): 1256-1269.

图/表 16

图1 正向模型

Fig.1 Forward model

图2 反向模型

Fig.2 Backward model

图3 含循环物流的信息流图

Fig.3 Information flow diagram with stream circulation

图4 断裂后的含循环物流的信息流图

Fig.4 Information flow diagram of stream circulation system after tearing stream

图5 求取收敛模块的流程图

Fig.5 The flow chart for obtaining convergence module

表1 劳斯表

Table 1 Rolls table

$w n$	$a n$	$a n - 2$	$a n - 4$	$a n - 6$	…
$w n - 1$	$a n - 1$	$a n - 3$	$a n - 5$	$a n - 7$	…
$w n - 2$	$b 1$	$b 2$	$b 3$	$b 4$	…
$w n - 3$	$c 1$	$c 2$	$c 3$	$c 4$	…
$w n - 4$	$d 1$	$d 2$	$d 3$	$d 4$	…
$?$	$?$	$?$	$?$	$?$	$?$
$w 2$	$e 1$	$e 2$
$w 1$	$f 1$	0
$w 0$	$g 1$	0

表1 劳斯表

Table 1 Rolls table

$w n$	$a n$	$a n - 2$	$a n - 4$	$a n - 6$	…
$w n - 1$	$a n - 1$	$a n - 3$	$a n - 5$	$a n - 7$	…
$w n - 2$	$b 1$	$b 2$	$b 3$	$b 4$	…
$w n - 3$	$c 1$	$c 2$	$c 3$	$c 4$	…
$w n - 4$	$d 1$	$d 2$	$d 3$	$d 4$	…
$?$	$?$	$?$	$?$	$?$	$?$
$w 2$	$e 1$	$e 2$
$w 1$	$f 1$	0
$w 0$	$g 1$	0

图6 甲苯氧化制苯甲酸反应-分离系统流程图

Fig.6 Schematic diagram of the reaction-separation cycle for the oxidation of toluene to benzoic acid

图7 反应-分离的信息流图

Fig.7 Information flow diagram for reaction-separation

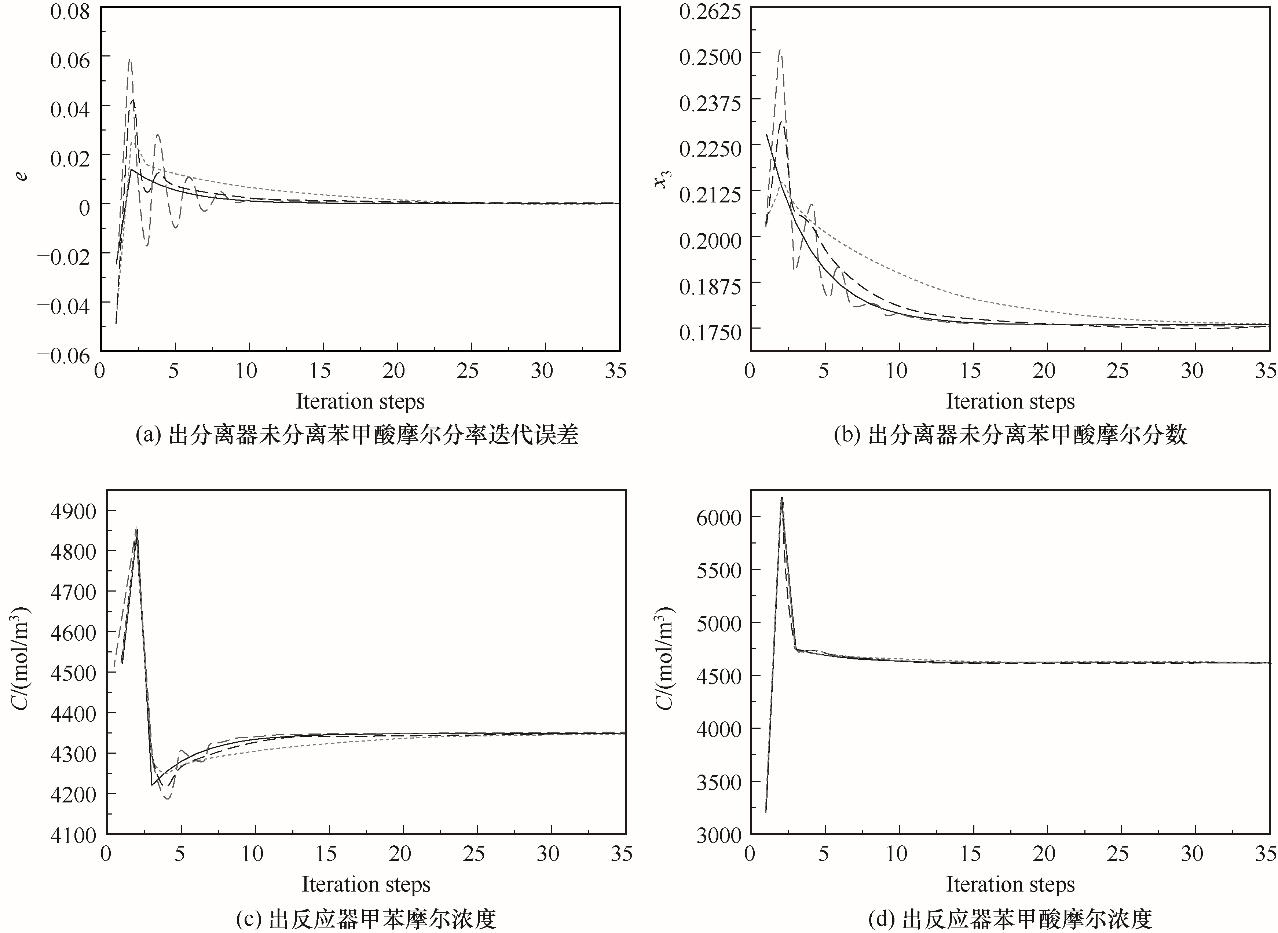
图8 甲苯氧化反应-分离系统四种模拟计算结果对比— 正向/反向模型迭代法; ---- 直接迭代法; -·- 加权迭代法; … 牛顿迭代法

Fig.8 Comparison simulation of four iterative methods for reaction-separation cycle of the toluene oxidation

图9 催化裂化装置结构示意图

Fig.9 Schematic diagram of FCCU

表2 催化裂化装置过程数据

Table 2 Process data of FCCU

压力/kPa		温度/℃
反应器顶	再生器顶	提升管出口	再生器密相床
244.95	274.38	500	700
催化剂藏量/ kg	主风流量/ (m³/h)	新鲜原料量/ (kg/h)	催化剂循环量/ (kg/h)
27000	45500	75000	410000

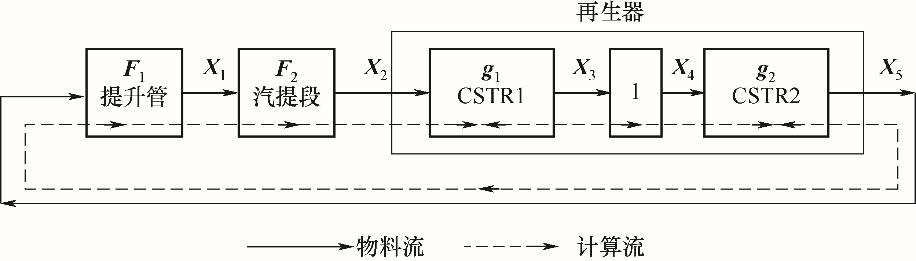
图10 催化裂化装置反应-再生系统的信息流X1——提升管出口变量; X2——再生器入口变量; X3——再生器第一个CSTR出口变量; X4——再生器第二个CSTR入口变量; X5——再生器第二个CSTR出口变量

Fig.10 Information flow diagram of the FCCU reaction-regeneration system

图11 断裂后催化裂化装置反应-再生系统的信息流

Fig.11 Information flow diagram of the FCCU reaction-regeneration system after tearing stream

图12 提升管与汽提段主要变量迭代收敛曲线

Fig.12 Iterative convergence curves for the main variables in riser and strip section

图13 再生器主要变量迭代收敛曲线

Fig.13 Iterative convergence curves for the main variables in regenerator

表3 本文模拟计算的稳态值和生产数据对比

Table 3 Comparison of simulated steady-state values and production data from this paper

各单元出口变量	模拟结果稳态值	生产数据	误差/%
再生剂含碳量/%(mass)	0.18	0.1875	4.00
再生温度/℃	699.85	700	0.02
再生烟气氧含量/%(mol)	2.66	2.77	3.97
反应温度/℃	503.39	500.0855	0.66
待生催化剂活性	0.2071	0.2030	0.02
汽提段出口焦炭含量/%(mass)	1.03	1	3.00
回炼油生成量/(t/h)	14.756	14.9500	1.30
回炼油油浆生成量/(t/h)	8.3908	8.5500	1.86
焦炭产率/%(mass)	4.7696	5.0104	4.81
柴油产率/%(mass)	39.9028	38.6386	3.27
汽油产率/%(mass)	39.5864	41.2439	4.02
气体产率/%(mass)	11.5450	12.1089	4.66

参考文献 41

1	张新强, 邱泽刚, 李志勤. 工艺流程模拟计算中循环物流的处理方法[J]. 化工设计通讯, 2019, 45(12): 129, 175.
	Zhang X Q, Qiu Z G, Li Z Q. Processing method for recycle materials in process simulation convergence[J]. Chemical Engineering Design Communications, 2019, 45(12): 129, 175.
2	Nikolopoulou A, Ierapetritou M G. Optimal design of sustainable chemical processes and supply chains: a review[J]. Computers & Chemical Engineering, 2012, 44: 94-103.
3	赵文, 周传光, 孙淑燕, 等. 反应-分离循环系统最佳工艺条件的确定[J]. 高校化学工程学报, 1999, 13(3): 245-251.
	Zhao W, Zhou C G, Sun S Y, et al. Optimal process condition of reaction-separation recycle system[J]. Journal of Chemical Engineering of Chinese Universities, 1999, 13(3): 245-251.
4	Jorissen F, Wetter M, Helsen L. Simplifications for hydronic system models in modelica[J]. Journal of Building Performance Simulation, 2018, 11(6): 639-654.
5	Adegbege A A, Heath W P. A framework for multivariable algebraic loops in linear anti-windup implementations[J]. Automatica, 2017, 83: 81-90.
6	Kozlowski A, Yamaguchi K. The homotopy type of the space of algebraic loops on a toric variety[J]. Topology and Its Applications, 2021, 300: 107705.
7	耿华, 杨耕. 控制系统仿真的代数环问题及其消除方法[J]. 电机与控制学报, 2006, 10(6): 632-635.
	Geng H, Yang G. Algebraic loop problems in simulations of control systems and the methods to avoid it[J]. Electric Machines and Control, 2006, 10(6): 632-635.
8	张毅超, 白建云. 一种改进型Smith预估补偿控制算法及其应用[J]. 自动化技术与应用, 2016, 35(10): 1-3, 13.
	Zhang Y C, Bai J Y. An improved Smith compensation control algorithm and its application[J]. Techniques of Automation and Applications, 2016, 35(10): 1-3, 13.
9	Hillestad M, Hertzberg T. Dynamic simulation of chemical engineering systems by the sequential modular approach[J]. Computers & Chemical Engineering, 1986, 10(4): 377-388.
10	Cao Y, He B S, Yan L B. Process simulation of a dual fluidized bed chemical looping air separation with Mn-based oxygen carrier[J]. Energy Conversion and Management, 2019, 196: 286-295.
11	Asadi-Saghandi H, Sheikhi A, Sotudeh-Gharebagh R. Sequence-based process modeling of fluidized bed biomass gasification[J]. ACS Sustainable Chemistry & Engineering, 2015, 3(11): 2640-2651.
12	王雅琳, 黎良伟, 桂卫华, 等. 序贯模块法在选矿流程模拟中的应用与实现[J]. 计算机工程与应用, 2009, 45(7): 224-226, 243.
	Wang Y L, Li L W, Gui W H, et al. Realization and application of mineral processing simulator using sequential modular approach[J]. Computer Engineering and Applications, 2009, 45(7): 224-226, 243.
13	占志良. 基于联立方程模型的乙烯淤浆聚合过程模拟与优化[D]. 杭州: 浙江大学, 2012.
	Zhan Z L. Simulation and optimization of an industrial HDPE slurry process based on equation oriented models[D]. Hangzhou: Zhejiang University, 2012.
14	俞裕国, 王长英. 氨合成回路的模拟分析与多目标优化的探讨[J]. 化工学报, 1988, 39(2): 129-136.
	Yu Y G, Wang C Y. Simulation and multi-objective optimization of ammonia synthesis loop[J]. Journal of Chemical Industry and Engineering (China), 1988, 39(2): 129-136.
15	刘广杰, 孙晓岩, 毕荣山, 等. 复杂炼油塔模拟的改进联立方程内外层算法[J]. 化工学报, 2020, 71(5): 2118-2127.
	Liu G J, Sun X Y, Bi R S, et al. Improved equation oriented inside-out method of complex crude distillation column simulation[J]. CIESC Journal, 2020, 71(5): 2118-2127.
16	胡仰栋, 刘芳芝, 周传光, 等. 联立方程法模拟多循环流程的新解算策略[J]. 化工学报, 1991, 42(1): 104-108.
	Hu Y D, Liu F Z, Zhou C G, et al. A new algorithm for simulation of multi-cycle processes by simultaneous equations method[J]. Journal of Chemical Industry and Engineering (China), 1991, 42(1): 104-108.
17	李云涛. 实际化工模拟过程有效切割算法的研究[J]. 炼油与化工, 2004, 15(2): 27-29, 45.
	Li Y T. Research on effective cutting algorithm during real chemical analog[J]. Refining and Chemicals, 2004, 15(2): 27-29, 45.
18	范超. 化工过程系统分隔与切断排序方法研究[D]. 北京: 北京化工大学, 2016.
	Fan C. Research on the method for partitioning and tearing sort of chemical process systems[D]. Beijing: Beijing University of Chemical Technology, 2016.
19	唐强. 精馏过程稳态模拟计算方法分析[J]. 化工设计通讯, 2020, 46(11): 81-82.
	Tang Q. Analysis of steady-state simulation of distillation process[J]. Chemical Engineering Design Communications, 2020, 46(11): 81-82.
20	Aliyu M D S. Iterative computational approach to the solution of the Hamilton-Jacobi-Bellman-Isaacs equation in nonlinear optimal control[J]. Control Theory and Technology, 2018, 16(1): 38-48.
21	Carson E, Higham N J. Accelerating the solution of linear systems by iterative refinement in three precisions[J]. SIAM Journal on Scientific Computing, 2018, 40(2): A817-A847.
22	Evans C, Pollock S, Rebholz L G, et al. A proof that Anderson acceleration improves the convergence rate in linearly converging fixed-point methods (but not in those converging quadratically)[J]. SIAM Journal on Numerical Analysis, 2020, 58(1): 788-810.
23	Li Y, Guo X P. Multi-step modified Newton-HSS methods for systems of nonlinear equations with positive definite Jacobian matrices[J]. Numerical Algorithms, 2017, 75(1): 55-80.
24	苏涛. 化工间歇过程的迭代学习控制方法[D]. 青岛: 青岛科技大学, 2014.
	Su T. Iterative learning control of chemical batch processes[D]. Qingdao, China: Qingdao University of Science & Technology, 2014.
25	Zhou W J, Shen D M. Convergence properties of an iterative method for solving symmetric non-linear equations[J]. Journal of Optimization Theory and Applications, 2015, 164(1): 277-289.
26	Geng Z Q, Wei C Y, Han Y M, et al. Pipeline network simulation calculation based on improved Newton Jacobian iterative method[C]//Proceedings of the 2019 International Conference on Artificial Intelligence and Computer Science. New York, USA: ACM, 2019: 219-223.
27	周游, 赵成业, 刘兴高. 一种求解化工动态优化问题的迭代自适应粒子群方法[J]. 化工学报, 2014, 65(4): 1296-1302.
	Zhou Y, Zhao C Y, Liu X G. An iteratively adaptive particle swarm optimization approach for solving chemical dynamic optimization problems[J]. CIESC Journal, 2014, 65(4): 1296-1302.
28	Kuo M T, Rubin D I. Optimization study of chemical processes[J]. The Canadian Journal of Chemical Engineering, 1962, 40(4): 152-156.
29	Shacham M, Kehat E. Converging interval methods for the iterative solution of a non-linear equation[J]. Chemical Engineering Science, 1973, 28(12): 2187-2193.
30	Motard R L, Shacham M, Rosen E M. Steady state chemical process simulation[J]. AIChE Journal, 1975, 21(3): 417-436.
31	Naseem A, Rehman M A, Abdeljawad T. Some new iterative algorithms for solving one-dimensional non-linear equations and their graphical representation[J]. IEEE Access, 2021, 9: 8615-8624.
32	汪德友, 崔艳雨, 李旭光, 等. 基于牛顿迭代法的复杂机坪管网水力计算[J]. 油气储运, 2020, 39(12): 1394-1400.
	Wang D Y, Cui Y Y, Li X G, et al. Hydraulic calculation for complicated apron pipeline network based on Newton iteration method[J]. Oil & Gas Storage and Transportation, 2020, 39(12): 1394-1400.
33	管慧莹. 求解非线性方程的两种迭代算法[D]. 哈尔滨: 哈尔滨理工大学, 2020.
	Guan H Y. Two iterative algorithms for solving nonlinear equations[D]. Harbin: Harbin University of Science and Technology, 2020.
34	王晓锋. 两类修正的3阶收敛的牛顿迭代格式[J]. 哈尔滨理工大学学报, 2011, 16(1): 113-115.
	Wang X F. Two classes of Newton's iteration methods with third-order convergence[J]. Journal of Harbin University of Science and Technology, 2011, 16(1): 113-115.
35	Fang X W, Ni Q, Zeng M L. A modified quasi-Newton method for nonlinear equations[J]. Journal of Computational and Applied Mathematics, 2018, 328: 44-58.
36	Bublitz S, Esche E, Tolksdorf G, et al. Analysis and decomposition for improved convergence of nonlinear process models in chemical engineering[J]. Chemie Ingenieur Technik, 2017, 89(11): 1503-1514.
37	罗雄麟. 前置烧焦罐式高效再生器催化裂化装置动态模拟与操作分析[D]. 北京: 中国石油大学, 1997.
	Luo X L. Dynamic modeling and operation analysis of FCCU(fluid catalytic cracking unit) with high efficient regenerator[D]. Beijing: China University of Petroleum, 1997.
38	罗雄麟, 袁璞, 林世雄. 催化裂化装置动态机理模型 (Ⅰ): 反应器部分[J]. 石油学报(石油加工), 1998, 14(1): 34
	Luo X L, Yuan P, Lin S X. Dynamic Model of Fluid Catalytic Cracking(Ⅰ): Reactor Section[J]. Acta Petrolei Sinica (Petroleum Processing Section), 1998, 14(1): 34
39	Zheng Y Y. Dynamic modeling and simulation of a catalytic cracking unit[J]. Computers & Chemical Engineering, 1994, 18(1): 39-44.
40	罗雄麟, 袁璞, 林世雄. 催化裂化装置动态机理模型 (Ⅱ): 再生器部分[J]. 石油学报(石油加工), 1998, 14(2): 34
	Luo X L, Yuan P, Lin S X. Dynamic Modeling of Fcc (Ⅱ): regenerator　section[J]. Acta Petrolei Sinica (Petroleum Processing Section), 1998, 14(2): 34
41	罗雄麟, 张建芳. 催化裂化高效再生器多级混合模型及其应用[J]. 石油炼制与化工, 1992, 23(8): 34-40.
	Luo X L, Zhang J F. A tanks-in-series model for the FCC regenerator with fast fluidization and its applications[J]. Petroleum Processing and Petrochemicals, 1992, 23(8): 34-40.

[1]	江河, 袁俊飞, 王林, 邢谷雨. 均流腔结构对微细通道内相变流动特性影响的实验研究[J]. 化工学报, 2023, 74(S1): 235-244.
[2]	陈哲文, 魏俊杰, 张玉明. 超临界水煤气化耦合SOFC发电系统集成及其能量转化机制[J]. 化工学报, 2023, 74(9): 3888-3902.
[3]	郑玉圆, 葛志伟, 韩翔宇, 王亮, 陈海生. 中高温钙基材料热化学储热的研究进展与展望[J]. 化工学报, 2023, 74(8): 3171-3192.
[4]	张瑞航, 曹潘, 杨锋, 李昆, 肖朋, 邓春, 刘蓓, 孙长宇, 陈光进. ZIF-8纳米流体天然气乙烷回收工艺的产品纯度关键影响因素分析[J]. 化工学报, 2023, 74(8): 3386-3393.
[5]	孟令玎, 崇汝青, 孙菲雪, 孟子晖, 刘文芳. 改性聚乙烯膜和氧化硅固定化碳酸酐酶[J]. 化工学报, 2023, 74(8): 3472-3484.
[6]	李贵贤, 曹阿波, 孟文亮, 王东亮, 杨勇, 周怀荣. 耦合固体氧化物电解槽的CO₂制甲醇过程设计与评价研究[J]. 化工学报, 2023, 74(7): 2999-3009.
[7]	毛磊, 刘冠章, 袁航, 张光亚. 可捕集CO₂的纳米碳酸酐酶粒子的高效制备及性能研究[J]. 化工学报, 2023, 74(6): 2589-2598.
[8]	蔡斌, 张效林, 罗倩, 党江涛, 左栗源, 刘欣梅. 导电薄膜材料的研究进展[J]. 化工学报, 2023, 74(6): 2308-2321.
[9]	邵远哲, 赵忠盖, 刘飞. 基于共同趋势模型的非平稳过程质量相关故障检测方法[J]. 化工学报, 2023, 74(6): 2522-2537.
[10]	徐文超, 孙志高, 李翠敏, 李娟, 黄海峰. 静态条件下表面活性剂E-1310对HCFC-141b水合物生成的影响[J]. 化工学报, 2023, 74(5): 2179-2185.
[11]	王子健, 柯明, 李佳涵, 李舒婷, 孙巾茹, 童燕兵, 赵治平, 刘加英, 任璐. 短b轴ZSM-5分子筛制备方法及应用研究进展[J]. 化工学报, 2023, 74(4): 1457-1473.
[12]	贠程, 王倩琳, 陈锋, 张鑫, 窦站, 颜廷俊. 基于社团结构的化工过程风险演化路径深度挖掘[J]. 化工学报, 2023, 74(4): 1639-1650.
[13]	陈向上, 马振杰, 任希华, 贾悦, 吕晓龙, 陈华艳. 三维网络萃取膜的制备及传质效率研究[J]. 化工学报, 2023, 74(3): 1126-1133.
[14]	顾学荣, 刘硕士, 杨思宇. 基于并行EGO和代理模型辅助的多参数优化方法研究[J]. 化工学报, 2023, 74(3): 1205-1215.
[15]	刘润竹, 储甜甜, 张孝阿, 王成忠, 张军营. α，ω-端羟基亚苯基氟硅聚合物的合成及性能[J]. 化工学报, 2023, 74(3): 1360-1369.