物理信息神经网络在两相流中的应用

doi:10.11949/0438-1157.20241241

摘要/Abstract

摘要：

机器学习和数据科学相关研究从计算机科学学科涌向化学工程，将为化学工程领域创造变革范式的机会，其中物理信息神经网络（PINN）因将物理方程嵌入神经网络中使得网络输出满足物理规律而获得广泛关注。首先介绍PINN的算法思想及其采样策略；进一步讨论对PINN的损失函数不同的处理方式，主要包括无观测值、方程降阶、方程离散化和只嵌入部分物理方程等；最后概述了PINN方法在气液两相流、多孔介质两相流、液固两相流、两相流传热等领域最新进展。

关键词: 流体力学, 多相流, 数值模拟, 物理信息神经网络, 采样策略, 损失函数

Abstract:

The influx of research on machine learning and data science from the field of computer science into chemical engineering presents transformative opportunities for chemical engineering paradigms. Among them, physics-informed neural network (PINN) has gained wide attention because it embeds physical equations into neural networks so that the network output satisfies physical laws. This work begins by introducing the algorithm ideas and sampling strategies of PINN. It further discuss various treatment of the PINN loss function, mainly including cases with no observational data, equation reduction, equation discretization, and partial embedding of physical equations. Finally, it provides an overview of recent progress in the application of PINN to areas such as gas-liquid two-phase flow, two-phase flow in porous media, liquid-solid two-phase flow, and heat transfer in two-phase flow.

Key words: fluid mechanics, multiphase flow, numerical simulation, physics-informed neural network, sampling strategy, loss function

中图分类号:

TQ 021.9

张橙, 李雪, 叶茂, 刘中民. 物理信息神经网络在两相流中的应用[J]. 化工学报, 2024, 75(11): 3835-3856.

Cheng ZHANG, Xue LI, Mao YE, Zhongmin LIU. Application of physics-informed neural network in two-phase flow[J]. CIESC Journal, 2024, 75(11): 3835-3856.

图/表 17

图1 用于偏微分方程的物理信息神经网络[48]

Fig.1 Physics-informed neural network for partial differential equation[48]

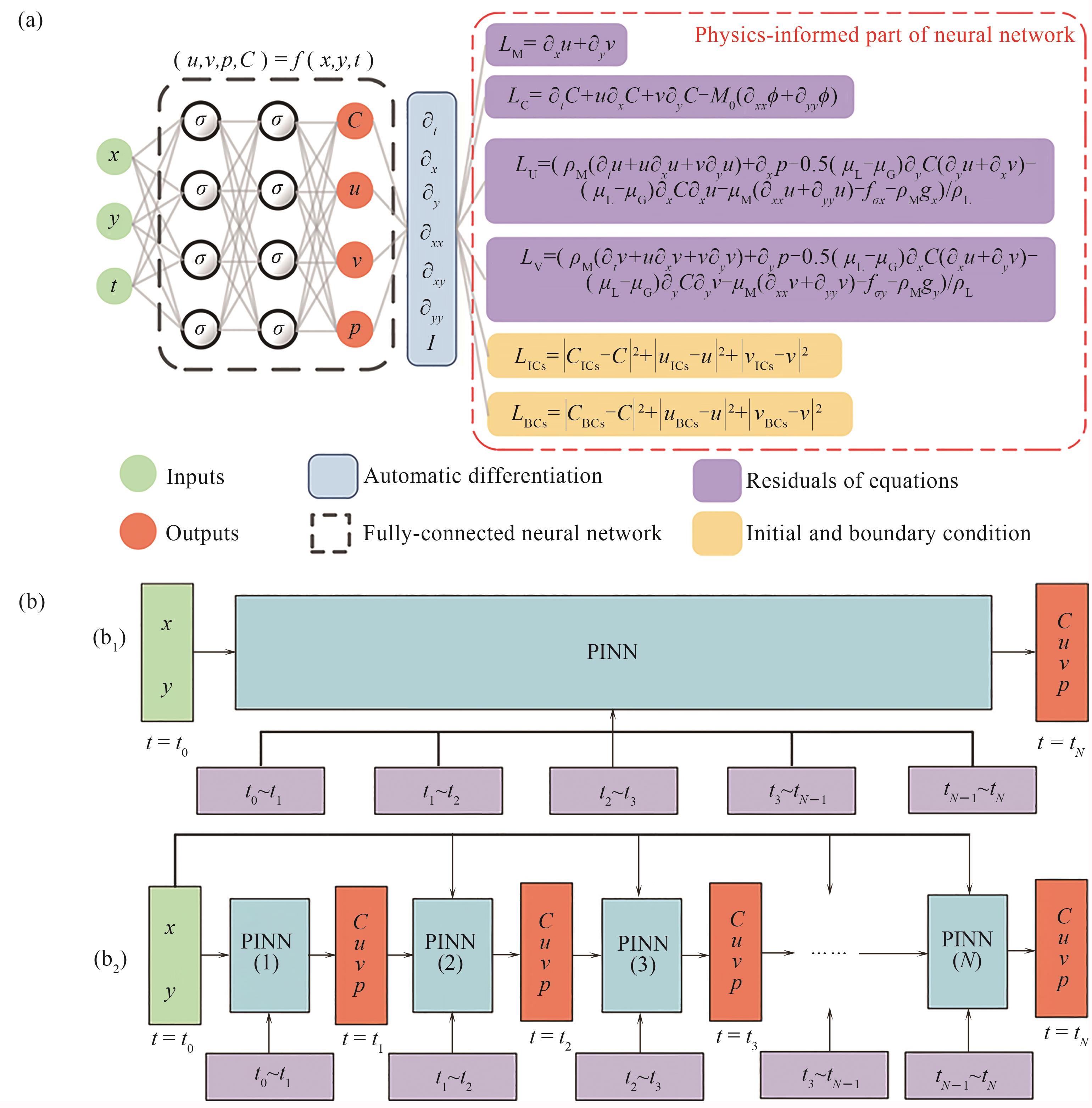
图2 (a)基于相场法的物理信息神经网络；(b)基于相场法的物理信息神经网络的不同时间推进策略：(b1)整个时间域内单网络训，(b2)在不同连续时间序列中的多网络训练[64]

Fig.2 (a) Illustration of physics-informed neural network for the phase-field method; (b) Different time marching strategies of physics-informed neural networks for the phase-field method: (b1) single network training in the whole time domain, (b2) multiple-networks training in various time sequences[64]

表1 普通形式神经网络与深度混合残差形式神经网络在界面演化方程中的区别［67］

Table 1 Differences between a normal neural network and a deep mixed residual method network in interface evolution equation［67］

\frac{\partial C}{\partial t} + (u \cdot \nabla) C = \nabla \cdot (M_{0} \nabla [C (C^{2} - 1) - ε^{2} \nabla^{2} C])

L = {‖\frac{\partial C}{\partial t} + (u \cdot \nabla) C - \nabla \cdot \{M_{0} \nabla [C (C^{2} - 1) - ε^{2} \nabla^{2} C]\}‖}_{2}^{2}

深度混合残差形式

$\frac{\partial C}{\partial t} + (u \cdot \nabla) C = \nabla \cdot (M_{0} \nabla ϕ)$

$ϕ = C (C^{2} - 1) - ε^{2} \nabla^{2} C$

L = {‖\frac{\partial C}{\partial t} + (u \cdot \nabla) C - \nabla \cdot (M_{0} \nabla ϕ)‖}_{2}^{2} + {‖ϕ - [C (C^{2} - 1) - ε^{2} \nabla^{2} C]‖}_{2}^{2}

表1 普通形式神经网络与深度混合残差形式神经网络在界面演化方程中的区别［67］

Table 1 Differences between a normal neural network and a deep mixed residual method network in interface evolution equation［67］

界面演化方程

显式形式

损失函数

普通形式

\frac{\partial C}{\partial t} + (u \cdot \nabla) C = \nabla \cdot (M_{0} \nabla [C (C^{2} - 1) - ε^{2} \nabla^{2} C])

L = {‖\frac{\partial C}{\partial t} + (u \cdot \nabla) C - \nabla \cdot \{M_{0} \nabla [C (C^{2} - 1) - ε^{2} \nabla^{2} C]\}‖}_{2}^{2}

深度混合残差形式

$\frac{\partial C}{\partial t} + (u \cdot \nabla) C = \nabla \cdot (M_{0} \nabla ϕ)$

$ϕ = C (C^{2} - 1) - ε^{2} \nabla^{2} C$

L = {‖\frac{\partial C}{\partial t} + (u \cdot \nabla) C - \nabla \cdot (M_{0} \nabla ϕ)‖}_{2}^{2} + {‖ϕ - [C (C^{2} - 1) - ε^{2} \nabla^{2} C]‖}_{2}^{2}

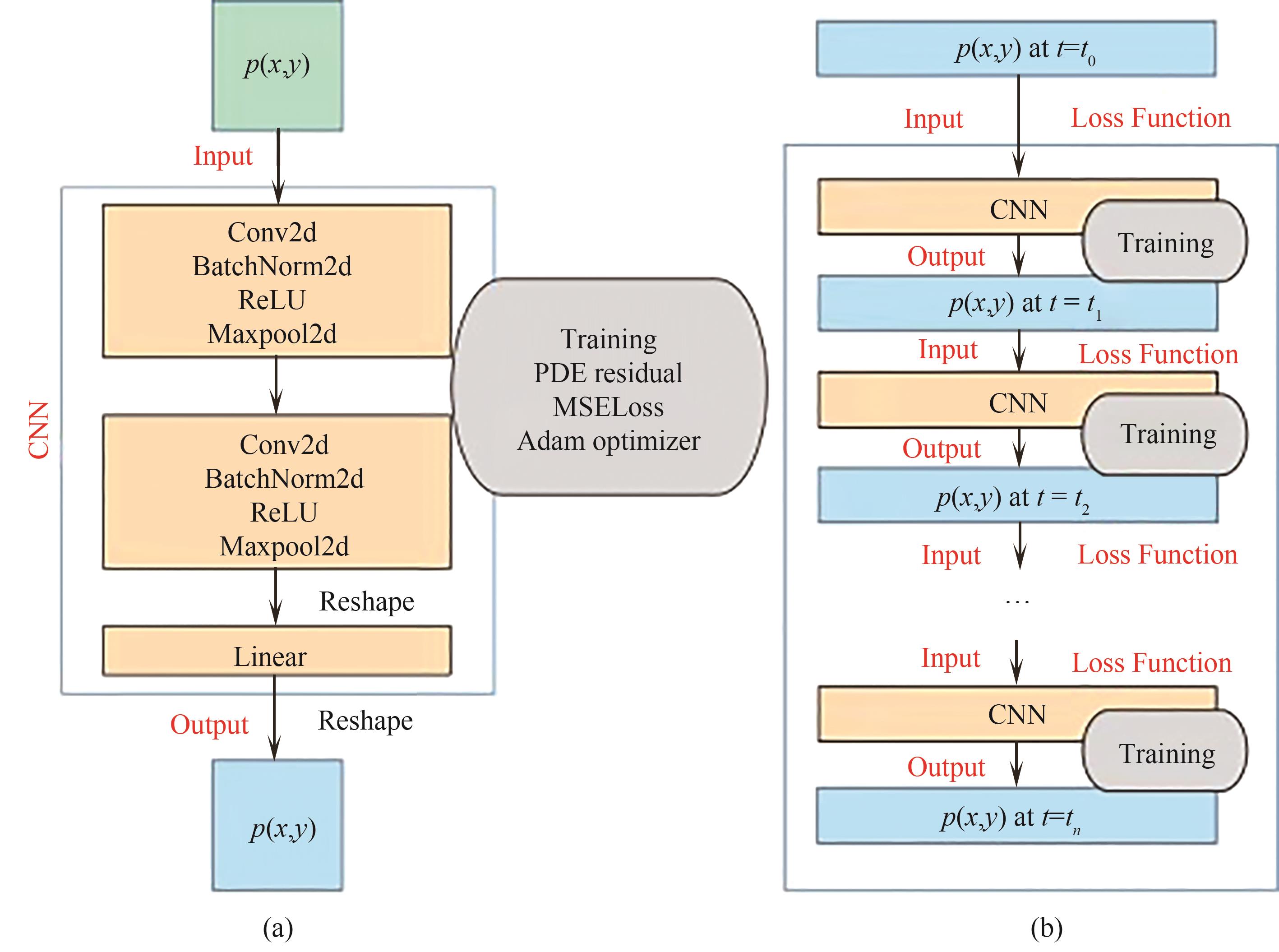
图3 (a) CNN结构作为模拟和数据同化的求解器; (b)基于PICNN的油藏模拟训练方案[68]

Fig.3 (a) The CNN structure as a solver for simulation and data assimilation; (b) The training scheme for PICNN-based reservoir simulation[68]

图4 半物理信息神经网络BubbleNet的框架[69]

Fig.4 Schematic diagram of the semi-physics-informed neural network BubbleNet[69]

图5 (a)单涡剪切流中基于相场法的物理信息神经网络相场变量C的预测值:(a1) t=0 s， (a2) t=0.5 s， (a3) t=1.0 s， (a4) t=1.5 s， (a5) t=2.0 s； (b)气泡上升算例中:气泡质心位置(b1)和气泡上升速度(b2)随时间变化关系（红实线代表基于相场法物理信息神经网络结果，蓝虚线代表来自Aland和Voigt的参考值）[64]

Fig.5 (a) Predicted results of phase-field variable C at a reverse single vortex based on physics-informed neural network for the phase-field method: (a1) t=0 s, (a2) t=0.5 s, (a3) t=1.0 s, (a4) t=1.5 s, (a5) t=2.0 s; (b) At bubble-rising problem: temporal evolution of bubble center of mass (b1) and rising velocity (b2) (the red solid lines correspond to the present result, while the blue dashed lines correspond to the reference result obtained from Aland and Voigt)[64]

图6 (a) RT不稳定性问题的计算区域和初始条件； (b) RT不稳定性问题：(b1)改进的PF-PINNs预测的相分数演化，(b2)文献结果[67]

Fig.6 (a) Computational domain and initial condition of RT instability; (b) Comparison of evolution of volume fraction of RT instability : (b1) results from modified PF-PINNs, (b2) results from reference[67]

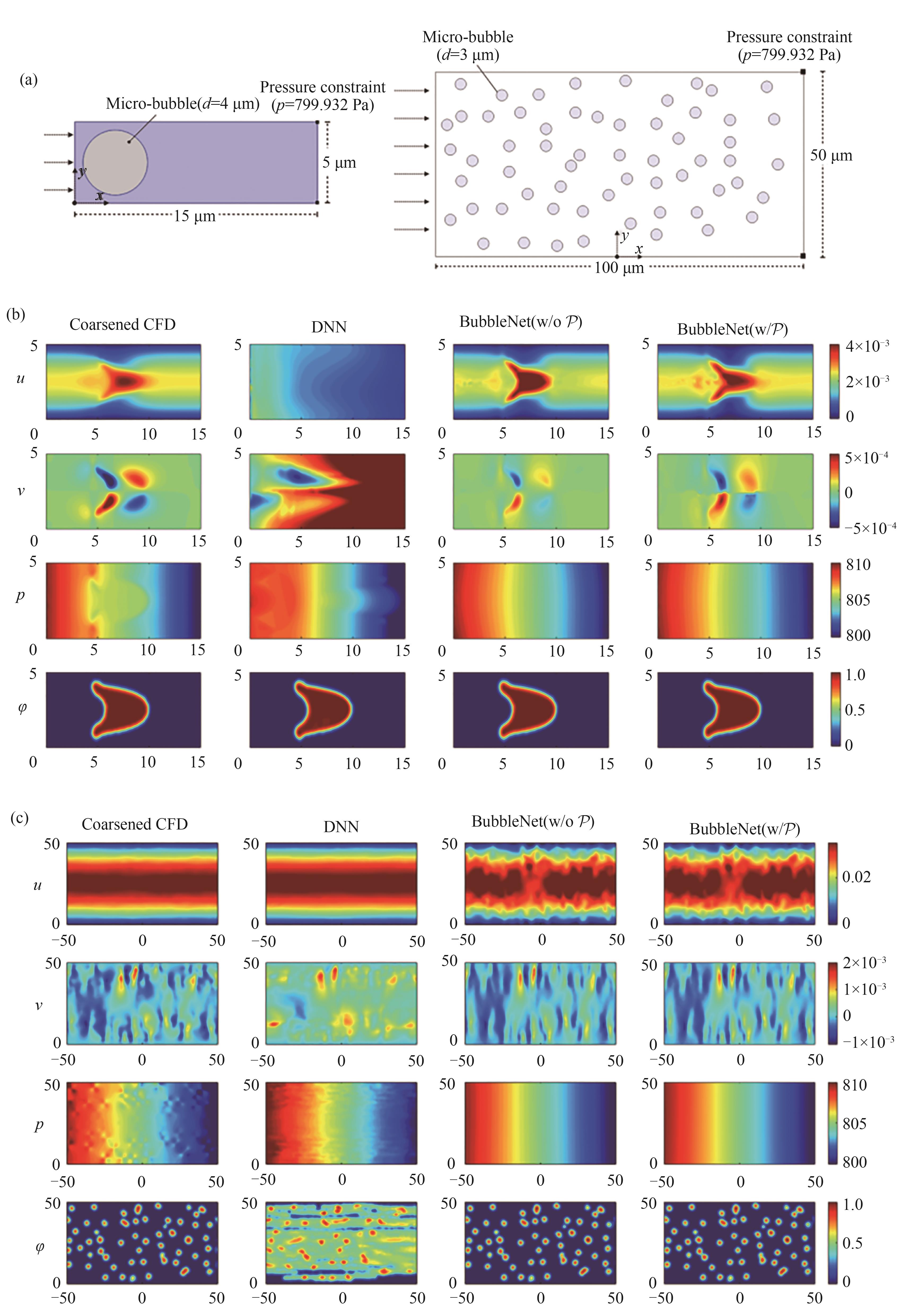
图7 (a)单气泡流和多气泡流的计算区域和初始条件；(b)单气泡流中CFD，DNN和BubbleNet中无、有泊松方程获得的物理量u，v，p，φ的比较；(c)多气泡流中CFD，DNN和BubbleNet中无、有泊松方程获得的物理量u，v，p，φ的比较[69]

Fig.7 (a) Computational domain and initial condition of single bubble flow case and multiple bubble flow case; (b) At single flow case: comparison of physical quantity u, v, p, φ between CFD, DNN, BubbleNet (without Poisson equation) and BubbleNet (with Poisson equation); (c) At multiple bubble flow case: comparison of physical quantity u, v, p, φ between CFD, DNN, BubbleNet (without Poisson equation) and BubbleNet (with Poisson equation)[69]

图8 (a) 一维计算区域和初始条件；(b) 二维计算区域和初始条件；(c) 一维示例中随着新的自适应性而演变的采样点（从左到右表示不同的控制方程，每个适应步骤后的新采样点用红色表示）[58]

Fig.8 (a) Initial condition of one-dimensional computational domain; (b) Initial condition of two-dimensional computational domain; (c) Evolution of collocation points with new adaptivity (from left to right represent different governing equations and new collocation points after each adaptation step are shown in red)[58]

图9 (a)注入井、采油井和边界条件的储层模型；(b)非均质油藏的渗透率场；(c)非均质油藏测试用例模拟结束时：压力场(c1)和含水饱和度场(c2)；(d)均匀油藏中采用PICNN方法和传统有限体积法得到的生产井井块压力和井底压力的变化[68]

Fig.9 (a) An illustration of the reservoir model with injector, producer and boundary conditions; (b) The permeability field for the heterogeneous test case; (c) The pressure (c1) and water saturation fields (c2) at the end of simulation for the heterogeneous test case; (d) The change of well-block and bottom-hole pressures of the producer obtained by PICNN for the heterogeneous reservoir, compared to reference solution by the conventional FV approach[68]

图10 (a)带有观测值的用于预测压力、气体饱和度和产水率的物理信息神经网络; (b)气体饱和度和(c)压力的真实值、预测值及相应的相对误差的比较：多输出训练(顶部)、基于物理信息无插值点(中间)和基于物理信息有插值点(底部)[71]

Fig.10 (a) Physics-informed neural network with observed values for prediction of pressure, gas saturation and water production;A comparison between the ground truth and predicted value together with the corresponding relative error for (b) gas saturation and (c) pressure field: multi-output data-driven model (top), physics-informed model without interpolated points (middle) and physics-informed model with interpolated points (bottom)[71]

表2 单输出训练（STT）、多输出训练（MTT）、基于物理信息无插值点（PI w/o interp）、基于物理信息有插值点（PI with interp）的MSE值（包括产水率、压力和气体饱和度）［71］

Table 2 Recorded MSE values （original un-normalized scale） for STT （single-output training）， MTT （multi-output training）， PI w/o interp（physics-informed without interpolated points）， PI with interp（physics-informed with interpolated points） for water production rate， pressure field and gas saturation field［71］

场	产水率	压力	气体饱和度
STT	1.05	0.13	$4.45 \times 10^{- 5}$
MTT	$1.40 \times 10^{- 2}$	$2.09 \times 10^{- 2}$	$2.43 \times 10^{- 5}$
PI w/o interp	$4.14 \times 10^{- 4}$	$2.35 \times 10^{- 2}$	$2.11 \times 10^{- 5}$
PI with interp	$2.52 \times 10^{- 4}$	$5.83 \times 10^{- 7}$	$6.03 \times 10^{- 6}$

场	产水率	压力	气体饱和度
STT	1.05	0.13	$4.45 \times 10^{- 5}$
MTT	$1.40 \times 10^{- 2}$	$2.09 \times 10^{- 2}$	$2.43 \times 10^{- 5}$
PI w/o interp	$4.14 \times 10^{- 4}$	$2.35 \times 10^{- 2}$	$2.11 \times 10^{- 5}$
PI with interp	$2.52 \times 10^{- 4}$	$5.83 \times 10^{- 7}$	$6.03 \times 10^{- 6}$

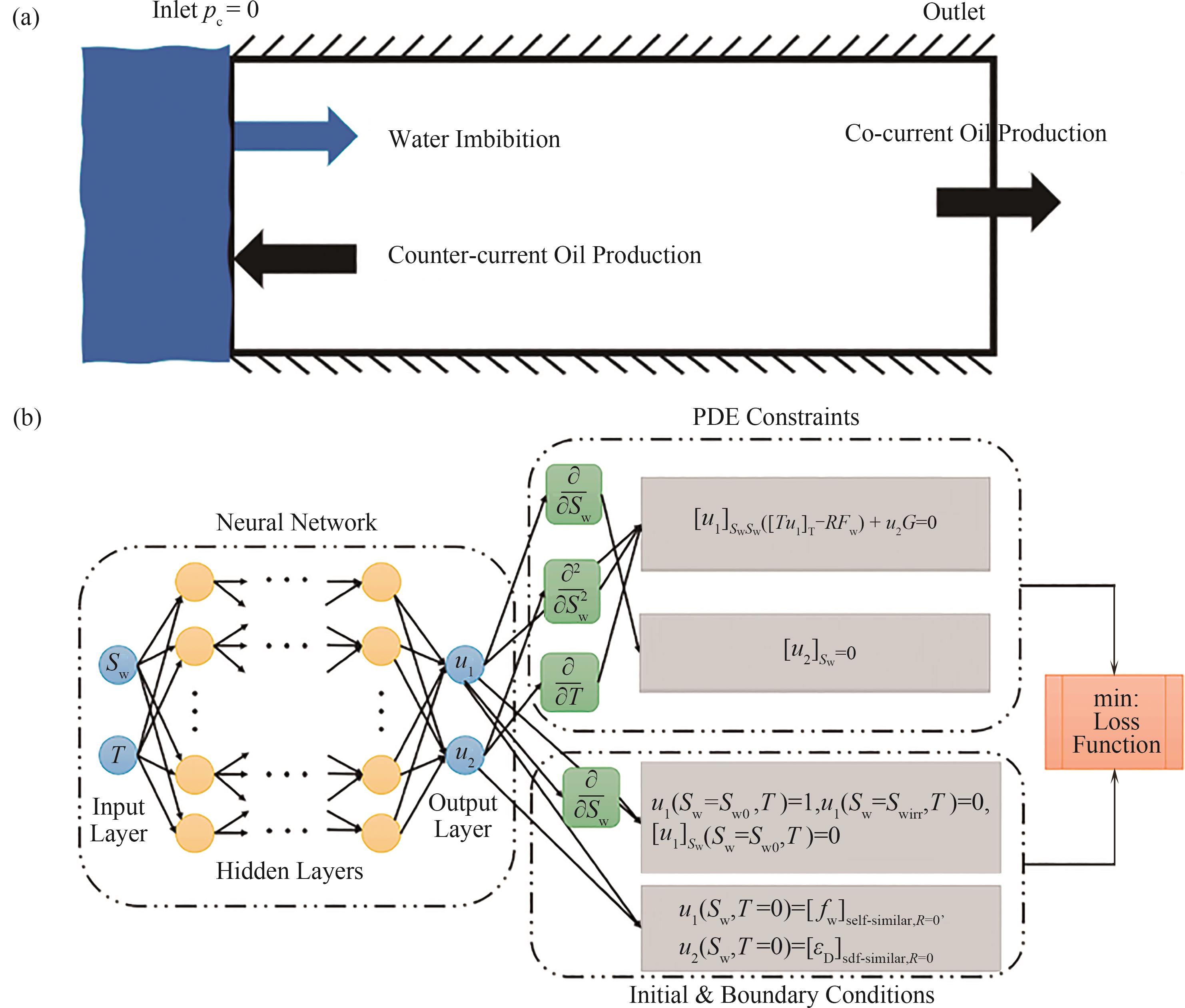
图11 (a)一维自发吸收设置；(b) 瞬态自发渗吸溶液的PINN架构[73]

Fig.11 (a) One-dimensional spontaneous imbibition configuration; (b) PINN configuration for self-similar spontaneous imbibition solution[73]

图12 (a) PINN预测的瞬时自发吸收平均归一化水通量；(b) PINN预测的瞬时自发吸收毛细管无量纲群；(c) PINN和有限差分间的平均归一化水通量的绝对误差；(d) PINN和有限差分间的毛细管无量纲群的绝对误差[73]

Fig.12 (a) PINN predicted average normalized water flux for transient spontaneous imbibition; (b) PINN predicted capillary dimensionless group for transient spontaneous imbibition; (c) Absolute difference in average normalized water flux between PINN and FD results for transient spontaneous imbibition; (d) Absolute difference in capillary dimensionless group between PINN and FD results for transient spontaneous imbibition [73]

图13 求解毛细管非均匀性的一维稳态两相流的PINN框架[74]

Fig.13 Schematic diagram of training the PINN system for solving two-phase steady state flow with capillary heterogeneity at various flow conditions[74]

图14 实际岩心驱替实验的1D饱和度剖面（红色十字）和PINN预测（黑色虚线），分流比为0.50 （a）、 0.80 (b)、 0.90 （c）和0.95 （d）[74]

Fig.14 1D saturation profiles of the actual core-flooding experiment (red crosses) and PINNs predictions (dotted black lines) at fractional flows of 0.50 (a), 0.80 (b), 0.90 (c), and 0.95 (d)[74]

图15 两相流传热PINN算法: (a) 网络架构; (b) 训练策略[75]

Fig.15 Configuration and training strategy of the PINN algorithm for heat transfer in two-phase flow: (a) network architecture; (b) training strategy[75]

参考文献 75

1	Dillard L A, Essaid H I, Herkelrath W N. Multiphase flow modeling of a crude-oil spill site with a bimodal permeability distribution[J]. Water Resources Research, 1997, 33(7): 1617-1632.
2	Gerritsen M G, Durlofsky L J. Modeling fluid flow in oil reservoirs[J]. Annual Review of Fluid Mechanics, 2005, 37(1): 211-238.
3	Ferdian E, Marlevi D, Schollenberger J, et al. Cerebrovascular super-resolution 4D Flow MRI-sequential combination of resolution enhancement by deep learning and physics-informed image processing to non-invasively quantify intracranial velocity, flow, and relative pressure[J]. Medical Image Analysis, 2023, 88: 102831.
4	Magnaudet J, Mercier M J. Particles, drops, and bubbles moving across sharp interfaces and stratified layers[J]. Annual Review of Fluid Mechanics, 2020, 52: 61-91.
5	Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225.
6	Chen L Q. Phase-field models for microstructure evolution[J]. Annual Review of Materials Research, 2002, 32: 113-140.
7	Karniadakis G E, Kevrekidis I G, Lu L, et al. Physics-informed machine learning[J]. Nature Reviews Physics, 2021, 3: 422-440.
8	Moreno Z, Paster A. Prediction of pollutant remediation in a heterogeneous aquifer in Israel: reducing uncertainty by incorporating lithological, head and concentration data[J]. Journal of Hydrology, 2018, 564: 651-666.
9	Moreno Z. Fine-scale heterogeneous structure impact on the scale-dependency of the effective hydro-electrical relations of unsaturated soils[J]. Advances in Water Resources, 2022, 162: 104156.
10	Moreno Z, Rabinovich A. Evaluating numerical simulation errors of CO₂-brine flow with capillary heterogeneity using a 1D semi-analytical solution[J]. International Journal of Greenhouse Gas Control, 2021, 110: 103416.
11	Brunton S L, Noack B R, Koumoutsakos P. Machine learning for fluid mechanics[J]. Annual Review of Fluid Mechanics, 2020, 52: 477-508.
12	Chang C W, Dinh N T. Classification of machine learning frameworks for data-driven thermal fluid models[J]. International Journal of Thermal Sciences, 2019, 135: 559-579.
13	Yan B C, Chen B L, Robert Harp D, et al. A robust deep learning workflow to predict multiphase flow behavior during geological CO₂ sequestration injection and Post-Injection periods[J]. Journal of Hydrology, 2022, 607: 127542.
14	Zhang K, Zuo Y D, Zhao H J, et al. Fourier neural operator for solving subsurface oil/water two-phase flow partial differential equation[J]. SPE Journal, 2022, 27(3): 1815-1830.
15	Montañez-Barrera J A, Barroso-Maldonado J M, Bedoya-Santacruz A F, et al. Correlated-informed neural networks: a new machine learning framework to predict pressure drop in micro-channels[J]. International Journal of Heat and Mass Transfer, 2022, 194: 123017.
16	Li W, Bazant M Z, Zhu J E. Phase-Field DeepONet: physics-informed deep operator neural network for fast simulations of pattern formation governed by gradient flows of free-energy functionals[J]. Computer Methods in Applied Mechanics and Engineering, 2023, 416: 116299.
17	Zhao X G, Shirvan K, Salko R K, et al. On the prediction of critical heat flux using a physics-informed machine learning-aided framework[J]. Applied Thermal Engineering, 2020, 164: 114540.
18	Seyed-Ahmadi A, Wachs A. Physics-inspired architecture for neural network modeling of forces and torques in particle-laden flows[J]. Computers & Fluids, 2022, 238: 105379.
19	Quintino A M, Da Rocha D L L N, Fonseca Junior R, et al. Flow pattern transition in pipes using data-driven and physics-informed machine learning. Journal of Fluids Engineering-Transactions of the Asme. 2021;143(3): 031401.
20	Wu Y Q, Sun S Y. Removing the performance bottleneck of pressure-temperature flash calculations during both the online and offline stages by using physics-informed neural networks[J]. 2023, 35(4): 043326.
21	Cheng Z H, Wachs A. Physics-informed neural network for modeling force and torque fluctuations in a random array of bidisperse spheres[J]. International Journal of Multiphase Flow, 2023, 169: 104603.
22	Dang Z R, Ishii M. Towards stochastic modeling for two-phase flow interfacial area predictions: a physics-informed reinforcement learning approach[J]. International Journal of Heat and Mass Transfer, 2022, 192: 122919.
23	Sirovich L. Turbulence and the dynamics of coherent structures (Ⅰ): Coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571.
24	Sirovich L, Kirby M. Low-dimensional procedure for the characterization of human faces[J]. Journal of the Optical Society of America A, 1987, 4(3): 519-524.
25	Kaiser E, Noack B R, Cordier L, et al. Cluster-based reduced-order modelling of a mixing layer[J]. Journal of Fluid Mechanics, 2014, 754: 365-414.
26	Colabrese S, Gustavsson K, Celani A, et al. Smart inertial particles[J]. Physical Review Fluids, 2018, 3(8): 084301.
27	Manohar K, Brunton B W, Kutz J N, et al. Data-driven sparse sensor placement for reconstruction: demonstrating the benefits of exploiting known patterns[J]. IEEE Control Systems Magazine, 2018, 38(3): 63-86.
28	Halko N, Martinsson P G, Tropp J A. Finding structure with randomness: probabilistic algorithms for constructing approximate matrix decompositions[J]. SIAM Review, 2011, 53(2): 217-288.
29	Dong C, Loy C C, He K M, et al. Learning a deep convolutional network for image super-resolution[M]//Lecture Notes in Computer Science. Cham: Springer International Publishing, 2014: 184-199.
30	Lee Y, Yang H, Yin Z P. PIV-DCNN: cascaded deep convolutional neural networks for particle image velocimetry[J]. Experiments in Fluids, 2017, 58(12): 171.
31	Xie Y, Franz E, Chu M Y, et al. tempoGAN: a temporally coherent, volumetric GAN for super-resolution fluid flow[EB/OL]. 2018: 1801.09710.
32	Mezić I. Analysis of fluid flows via spectral properties of the koopman operator[J]. Annual Review of Fluid Mechanics, 2013, 45: 357-378.
33	Schmid P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanics, 2010, 656: 5-28.
34	Raissi M, Karniadakis G E. Hidden physics models: machine learning of nonlinear partial differential equations[J]. Journal of Computational Physics, 2018, 357: 125-141.
35	Schmidt M, Lipson H. Distilling free-form natural laws from experimental data[J]. Science, 2009, 324(5923): 81-85.
36	Ling J L, Jones R, Templeton J. Machine learning strategies for systems with invariance properties[J]. Journal of Computational Physics, 2016, 318: 22-35.
37	Ling J L, Kurzawski A, Templeton J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance[J]. Journal of Fluid Mechanics, 2016, 807: 155-166.
38	Raissi M, Wang Z C, Triantafyllou M S, et al. Deep learning of vortex-induced vibrations[J]. Journal of Fluid Mechanics, 2019, 861: 119-137.
39	Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707.
40	Huang Y, Zhang Z Y, Zhang X. A direct-forcing immersed boundary method for incompressible flows based on physics-informed neural network[J]. Fluids, 2022, 7(2): 56.
41	Shukla K, Jagtap A D, Karniadakis G E. Parallel physics-informed neural networks via domain decomposition[J]. Journal of Computational Physics, 2021, 447: 110683.
42	Raissi M, Yazdani A, Karniadakis G E. Hidden fluid mechanics: learning velocity and pressure fields from flow visualizations[J]. Science, 2020, 367(6481): 1026-1030.
43	Bararnia H, Esmaeilpour M. On the application of physics informed neural networks (PINN) to solve boundary layer thermal-fluid problems[J]. International Communications in Heat and Mass Transfer, 2022, 132: 105890.
44	Cai S Z, Wang Z C, Fuest F, et al. Flow over an espresso cup: inferring 3-D velocity and pressure fields from tomographic background oriented schlieren via physics-informed neural networks[J]. Journal of Fluid Mechanics, 2021, 915: A102.
45	Laubscher R. Simulation of multi-species flow and heat transfer using physics-informed neural networks[J]. Physics of Fluids, 2021, 33(8): 087101.
46	Laubscher R, Rousseau P. Application of a mixed variable physics-informed neural network to solve the incompressible steady-state and transient mass, momentum, and energy conservation equations for flow over in-line heated tubes[J]. Applied Soft Computing, 2022, 114: 108050.
47	Cai S Z, Mao Z P, Wang Z C, et al. Physics-informed neural networks (PINNs) for fluid mechanics: a review[J]. Acta Mechanica Sinica, 2021, 37(12): 1727-1738.
48	Bradley W, Kim J, Kilwein Z, et al. Perspectives on the integration between first-principles and data-driven modeling[J]. Computers & Chemical Engineering, 2022, 166: 107898.
49	Díez P, Huerta A. A unified approach to remeshing strategies for finite element h-adaptivity[J]. Computer Methods in Applied Mechanics and Engineering, 1999, 176(1/2/3/4): 215-229.
50	Askes H, Rodríguez-Ferran A. A combined rh-adaptive scheme based on domain subdivision. Formulation and linear examples[J]. International Journal for Numerical Methods in Engineering, 2001, 51(3): 253-273.
51	Babuška I, Suri M. The p and h-p versions of the finite element method, basic principles and properties[J]. SIAM Review, 1994, 36(4): 578-632.
52	Zhang X D, Trépanier J Y, Camarero R. A posteriori error estimation for finite-volume solutions of hyperbolic conservation laws[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 185(1): 1-19.
53	McRae D S. R-Refinement grid adaptation algorithms and issues[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 189(4): 1161-1182.
54	Lee D, Tsuei Y M. A formula for estimation of truncation errors of convection terms in a curvilinear coordinate system[J]. Journal of Computational Physics, 1992, 98(1): 90-100.
55	Choudhary A, Roy C. Efficient residual-based mesh adaptation for 1D and 2D CFD applications[C]∥49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Florida, 2011.
56	Roy C. Strategies for driving mesh adaptation in CFD[C]∥47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Florida, 2009.
57	Lu L, Meng X H, Mao Z P, et al. Deep XDE: a deep learning library for solving differential equations[J]. SIAM Review, 2021, 63(1): 208-228.
58	Hanna J M, Aguado J V, Comas-Cardona S, et al. Residual-based adaptivity for two-phase flow simulation in porous media using Physics-informed Neural Networks[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 396: 115100.
59	Gurtin M E, Polignone D, Viñals J. Two-phase binary fluids and immiscible fluids described by an order parameter[J]. Mathematical Models and Methods in Applied Sciences, 1996, 6(6): 815-831.
60	Ma C, Wu J, Zhang T W. A high order spectral difference-based phase field lattice Boltzmann method for incompressible two-phase flows[J]. Physics of Fluids, 2020, 32(12): 122113.
61	Kou J S, Wang X H, Zeng M L, et al. Energy stable and mass conservative numerical method for a generalized hydrodynamic phase-field model with different densities[J]. Physics of Fluids, 2020, 32(11): 117103.
62	Dadvand A, Bagheri M, Samkhaniani N, et al. Advected phase-field method for bounded solution of the Cahn-Hilliard Navier-Stokes equations[J]. Physics of Fluids, 2021, 33(5): 053311.
63	De Rosis A, Enan E. A three-dimensional phase-field lattice Boltzmann method for incompressible two-components flows[J]. Physics of Fluids, 2021, 33(4): 043315.
64	Qiu R D, Huang R F, Xiao Y, et al. Physics-informed neural networks for phase-field method in two-phase flow[J]. Physics of Fluids, 2022, 34(5): 052109.
65	Zhao C L W, Jia. Solving Allen-cahn and cahn-Hilliard equations using the adaptive physics informed neural networks[J]. Communications in Computational Physics, 2021, 29(3): 930-954.
66	Lyu L Y, Zhang Z, Chen M X, et al. MIM: a deep mixed residual method for solving high-order partial differential equations[J]. Journal of Computational Physics, 2022, 452: 110930.
67	丘润荻, 王静竹, 黄仁芳, 等. 改进的物理融合神经网络在瑞利-泰勒不稳定性问题中的应用[J]. 力学学报, 2022, 54(8): 2224-2234.
	Qiu R D, Wang J Z, Huang R F, et al. The application of modified physics-informed neural networks in Rayleigh-Taylor instability[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(8): 2224-2234.
68	Zhang Z, Yan X, Liu P Y, et al. A physics-informed convolutional neural network for the simulation and prediction of two-phase Darcy flows in heterogeneous porous media[J]. Journal of Computational Physics, 2023, 477: 111919.
69	Zhai H F, Zhou Q, Hu G H. Predicting micro-bubble dynamics with semi-physics-informed deep learning[J]. AIP Advances, 2022, 12(3): 035153.
70	Yan X, Lin J Q, Wang S, et al. Physics-informed neural network simulation of two-phase flow in heterogeneous and fractured porous media[J]. Advances in Water Resources, 2024, 189: 104731.
71	Shokouhi P, Kumar V, Prathipati S, et al. Physics-informed deep learning for prediction of CO₂ storage site response[J]. Journal of Contaminant Hydrology, 2021, 241: 103835.
72	Sheremetov L, Lopez-Peña L A, Díaz-Cortes G B, et al. Deep learning model of two-phase fluid transport through fractured media: a real-world case study[M]//Lecture Notes in Computer Science. Cham: Springer Nature Switzerland, 2024: 55-68.
73	Deng L C, Pan Y W. Application of physics-informed neural networks for self-similar and transient solutions of spontaneous imbibition[J]. Journal of Petroleum Science and Engineering, 2021, 203: 108644.
74	Chakraborty A, Rabinovich A, Moreno Z. Physics-informed neural networks for modeling two-phase steady state flow with capillary heterogeneity at varying flow conditions[J]. Advances in Water Resources, 2024, 185: 104639.
75	Jalili D, Jang S, Jadidi M, et al. Physics-informed neural networks for heat transfer prediction in two-phase flows[J]. International Journal of Heat and Mass Transfer, 2024, 221: 125089.

[1]	董新宇, 边龙飞, 杨怡怡, 张宇轩, 刘璐, 王腾. 冷却条件下倾斜上升管S-CO₂流动与传热特性研究[J]. 化工学报, 2024, 75(S1): 195-205.
[2]	郭骐瑞, 任丽媛, 陈康, 黄翔宇, 马卫华, 肖乐勤, 周伟良. 用于HTPB推进剂浆料的静态混合管数值模拟[J]. 化工学报, 2024, 75(S1): 206-216.
[3]	李匡奚, 于佩潜, 王江云, 魏浩然, 郑志刚, 冯留海. 微气泡旋流气浮装置内流动分析与结构优化[J]. 化工学报, 2024, 75(S1): 223-234.
[4]	汪张洲, 唐天琪, 夏嘉俊, 何玉荣. 基于复合相变材料的电池热管理性能模拟[J]. 化工学报, 2024, 75(S1): 329-338.
[5]	胡俭, 姜静华, 范生军, 刘建浩, 邹海江, 蔡皖龙, 王沣浩. 中深层U型地埋管换热器取热特性研究[J]. 化工学报, 2024, 75(S1): 76-84.
[6]	任冠宇, 张义飞, 李新泽, 杜文静. 翼型印刷电路板式换热器流动传热特性数值研究[J]. 化工学报, 2024, 75(S1): 108-117.
[7]	李焱, 郑利军, 张恩勇, 王云飞. 深水海底管道软管内部流体渗透特性模型与试验研究[J]. 化工学报, 2024, 75(S1): 118-125.
[8]	杨勇, 祖子轩, 李煜坤, 王东亮, 范宗良, 周怀荣. T型圆柱形微通道内CO₂碱液吸收数值模拟[J]. 化工学报, 2024, 75(S1): 135-142.
[9]	黄俊豪, 庞克亮, 孙方远, 刘福军, 谷致远, 韩龙, 段衍泉, 冯妍卉. 干熄炉料钟结构对焦炭布料粒径均匀度影响的模拟研究[J]. 化工学报, 2024, 75(S1): 158-169.
[10]	李舒月, 王欢, 周少强, 毛志宏, 张永民, 王军武, 吴秀花. 基于CPFD方法的U₃O₈氢还原流化床反应器数值模拟[J]. 化工学报, 2024, 75(9): 3133-3151.
[11]	祝赫, 张仪, 齐娜娜, 张锴. 欧拉-欧拉双流体模型中颗粒黏性对液固散式流态化的影响[J]. 化工学报, 2024, 75(9): 3103-3112.
[12]	陈巨辉, 苏潼, 李丹, 陈立伟, 吕文生, 孟凡奇. 翅形扰流片作用下的微通道换热特性[J]. 化工学报, 2024, 75(9): 3122-3132.
[13]	钱啸宇, 阮璇, 李水清. 外加电场下电介质颗粒层结构重构与悬浮[J]. 化工学报, 2024, 75(8): 2756-2762.
[14]	朱子良, 王爽, 姜宇昂, 林梅, 王秋旺. 欧拉-拉格朗日迭代固-液相变算法[J]. 化工学报, 2024, 75(8): 2763-2776.
[15]	邓爱明, 何玉荣, 唐天琪, 胡彦伟. 导流板对喷雾流化床内颗粒生长过程影响的模拟[J]. 化工学报, 2024, 75(8): 2787-2799.