遗传算法在催化体系的全局结构优化中的应用

doi:10.11949/0438-1157.20201037

摘要/Abstract

摘要：

对催化体系进行全局结构优化，搜寻基态结构对预测催化剂结构、分析反应物的吸附特性、研究多相催化反应机理、构建实际反应路径等方面至关重要。遗传算法通过交叉、变异和选择等操作，模拟了自然淘汰进化过程，来搜索势能面上的基态结构。作为一种无偏优化算法，遗传算法的优化过程不依赖于输入结构，具有很强的全局搜索能力。对遗传算法在催化体系的全局结构优化问题中的应用进行了综述，介绍了遗传算法在实空间上进行全局结构优化的基本程序框架以及近年来结合并行计算、机器学习等技术发展的改进框架，并讨论了它们在团簇优化、负载型催化剂的结构优化问题上的相关应用，为遗传算法的进一步改进以及更广泛的应用提供理论指导。

关键词: 遗传算法, 全局优化, 催化, 势能面, 纳米结构, 分子模拟, 机器学习

Abstract:

Genetic algorithm is widely used to search for the global minimum structure that is important for analyzing the catalyst structure, the mechanism of heterogeneous catalytic reaction, and actual reaction pathway. By performing crossover, mutation and selection, genetic algorithm reflects the process of natural selection where the fittest individuals are selected for reproduction to explore the potential energy surface. As an unbiased optimization algorithm, the optimization process of genetic algorithm does not depend on the input structure and has strong global search capabilities. This review summarizes the recent progress of the design and application of genetic algorithm, as a global structure optimizer, in the catalytic system. Starting with introducing the standard genetic algorithm framework for global structure optimization, this review also includes the advanced framework developed by introducing parallel computing and machine learning technique. Finally, some examples about the reported application of genetic algorithm in catalytic structure optimization are presented, such as the optimization of metallic clusters, supported catalysts, etc. This review might provide a significant insight into the further improvement of genetic algorithm and the wider application in catalytic system.

Key words: genetic algorithm, global optimization, catalysis, potential energy surface, nanostructure, molecular simulation, machine learning

中图分类号:

O 643

石向成, 赵志坚, 巩金龙. 遗传算法在催化体系的全局结构优化中的应用[J]. 化工学报, 2021, 72(1): 27-41.

SHI Xiangcheng, ZHAO Zhijian, GONG Jinlong. Application of genetic algorithm in the global structure optimization of catalytic system[J]. CIESC Journal, 2021, 72(1): 27-41.

图/表 10

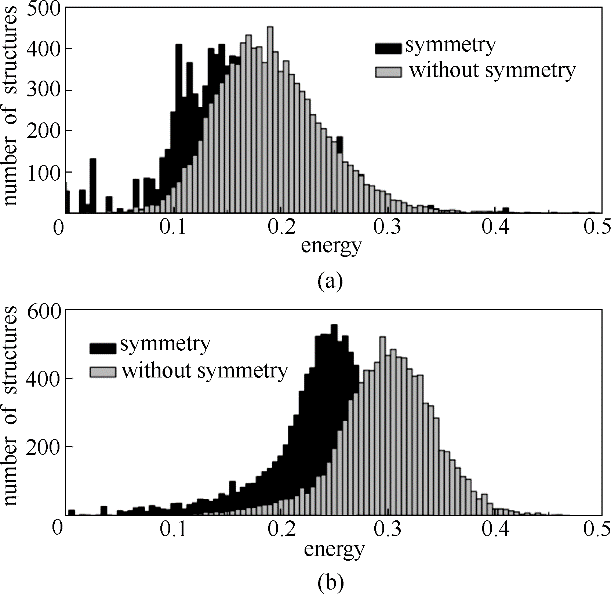
图1 包含和不包含对称性时随机产生的LJ38(a)和LJ100(b)团簇的能量分布（能量值是相对基态结构的相对值）[29]

Fig.1 Energetic distributions of randomly generated structures for LJ38 (a) and LJ100 (b) clusters with and without symmetry（energies are shown relative to the global minimum）[29]

图2 父代通过几何剪贴法交叉形成新子代的过程

Fig.2 The cut-and-splice pairing used on the crossover process for the generation of new structure

图3 基于池的遗传算法框架及其性能测试[21]

Fig.3 The framework of pool-GA and its performance test results

图4 结合主动学习进行加速的遗传算法框架及性能表现

Fig.4 Flowchart for the active learning-accelerated genetic algorithm method and its performance test results

图5 不同尺寸和电荷下的Au团簇的基态结构

Fig.5 The global minimum structure of Au cluster with different size

图6 不同尺寸硫醇配体保护的Au团簇及其成核、成长过程[4]

Fig.6 Schematic illustrations of the size-evolution of Aum(SR)n clusters

图7 遗传算法所得到的各类负载型催化剂的基态结构

Fig.7 The global minimum structure of supported catalyst generated by genetic algorithm

图8 Pt7团簇在α-Al2O3表面上的演化过程[9]

Fig.8 The evolutionary process of Pt7 cluster on α-Al2O3 surface[9]

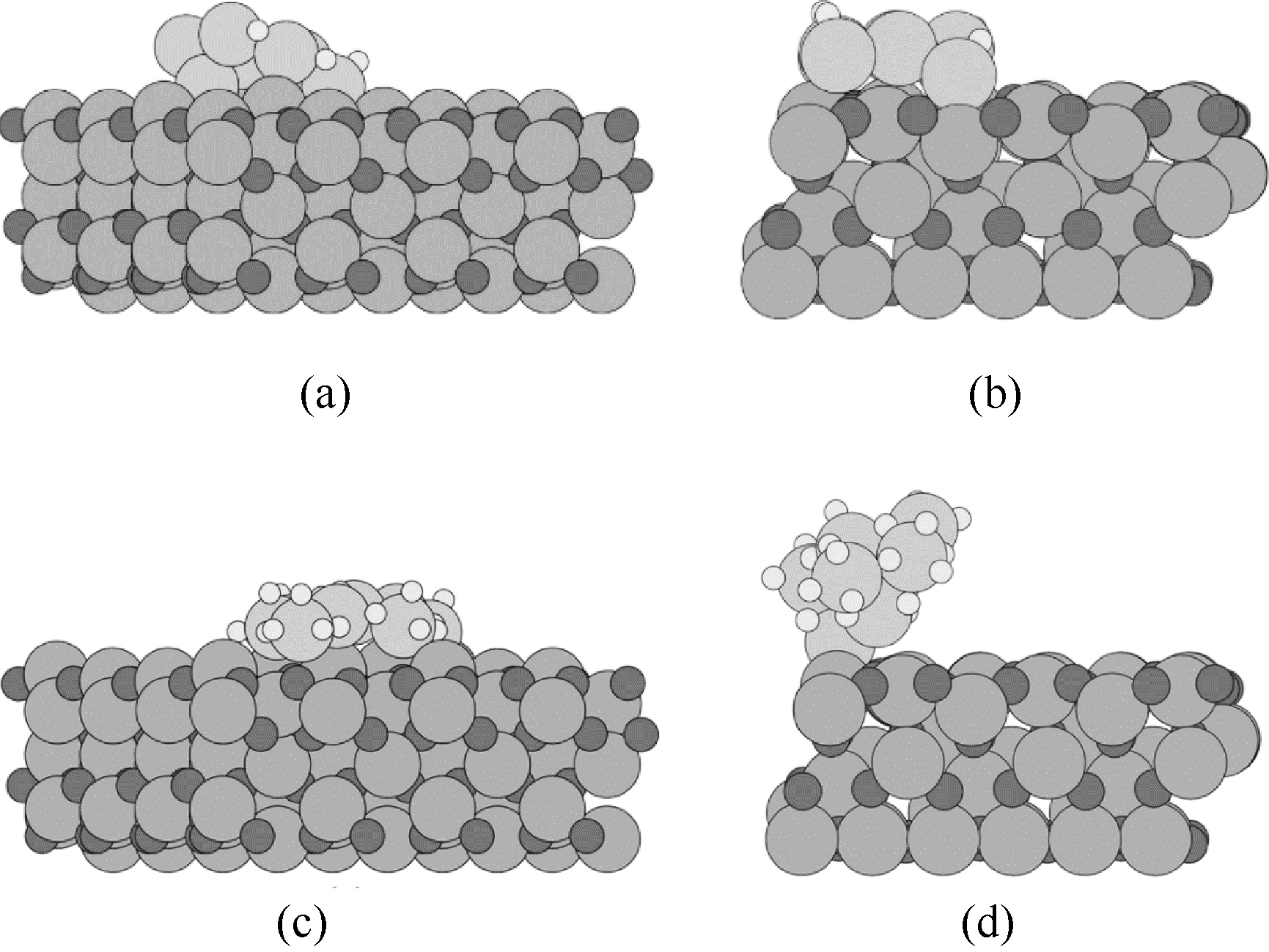
图9 α-Al2O3(0001)吸附的Pt8H4团簇(a)，γ-Al2O3(100)吸附的Pt8H5团簇(b)，α-Al2O3(0001)吸附的Pt8H24团簇(c)和γ-Al2O3(100)吸附的Pt8H24团簇(d)的基态结构[91]

Fig.9 Global minimum structure of Pt8H4 on α-Al2O3(0001) (a), Pt8H5 on γ-Al2O3(100) (b), Pt8H24 on α-Al2O3(0001) (c), and Pt8H24 on γ-Al2O3(100) (d)[91]

图10 O2在MgO(100)负载的Au12团簇的吸附过程[92]

Fig.10 The adsorption process of O2 on the MgO(100)-supported Au12 clusters[92]

参考文献 92

1	Johnston R L. Evolving better nanoparticles: genetic algorithms for optimising cluster geometries[J]. Dalton Transactions, 2003, (22): 4193-4207.
2	Mcleod A S, Gladden L F. Heterogeneous catalyst design using stochastic optimization algorithms[J]. Journal of Chemical Information and Computer Sciences, 2000, 40(4): 981-987.
3	Davis J B A, Horswell S L, Johnston R L. Application of a parallel genetic algorithm to the global optimization of gas-phase and supported gold–iridium sub-nanoalloys[J]. The Journal of Physical Chemistry C, 2016, 120(7): 3759-3765.
4	Liu C, Pei Y, Sun H, et al. The nucleation and growth mechanism of thiolate-protected Au nanoclusters[J]. Journal of the American Chemical Society, 2015, 137(50): 15809-15816.
5	Reichenbach T, Walter M, Moseler M, et al. Effects of gas-phase conditions and particle size on the properties of Cu(111)-supported Zn_yO_x particles revealed by global optimization and ab initio thermodynamics[J]. The Journal of Physical Chemistry C, 2019, 123(51): 30903-30916.
6	Fang Y, Gong X. Genetic algorithm aided density functional theory simulations unravel the kinetic nature of Au(100) in catalytic CO oxidation[J]. Chinese Chemical Letters, 2019, 30(6): 1346-1350.
7	Ding X L, Liao H L, Zhang Y, et al. Geometric and electronic properties of gold clusters doped with a single oxygen atom[J]. Physical Chemistry Chemical Physics, 2016, 18(41): 28960-28972.
8	Zandkarimi B, Alexandrova A N. Dynamics of subnanometer Pt clusters can break the scaling relationships in catalysis[J]. The Journal of Physical Chemistry Letters, 2019, 10(3): 460-467.
9	Zhai H, Alexandrova A N. Local fluxionality of surface-deposited cluster catalysts: the case of Pt₇ on Al₂O₃[J]. The Journal of Physical Chemistry Letters, 2018, 9(7): 1696-1702.
10	Jäger M, Schäfer R, Johnston R L. First principles global optimization of metal clusters and nanoalloys[J]. Advances in Physics: X, 2018, 3(1): 1516514.
11	Stillinger F H. Exponential multiplicity of inherent structures[J]. Physical Review E, 1999, 59(1): 48-51.
12	Sierka M. Synergy between theory and experiment in structure resolution of low-dimensional oxides[J]. Progress in Surface Science, 2010, 85(9/10/11/12): 398-434.
13	Hartke B. Global geometry optimization of clusters using genetic algorithms[J]. The Journal of Physical Chemistry, 1993, 97(39): 9973-9976.
14	Deaven D M, Ho K M. Molecular geometry optimization with a genetic algorithm[J]. Physical Review Letters, 1995, 75(2): 288-291.
15	Froemming N S, Henkelman G. Optimizing core-shell nanoparticle catalysts with a genetic algorithm[J]. The Journal of Chemical Physics, 2009, 131(23): 234103.
16	Vilhelmsen L B, Hammer B. A genetic algorithm for first principles global structure optimization of supported nano structures[J]. The Journal of Chemical Physics, 2014, 141(4): 044711.
17	Yang H, Wong M W. Automatic conformational search of transition states for catalytic reactions using genetic algorithm[J]. The Journal of Physical Chemistry A, 2019, 123(47): 10303-10314.
18	Dittner M, Hartke B. Globally optimal catalytic fields – inverse design of abstract embeddings for maximum reaction rate acceleration[J]. Journal of Chemical Theory and Computation, 2018, 14(7): 3547-3564.
19	Hartke B. Global cluster geometry optimization by a phenotype algorithm with niches: location of elusive minima, and low-order scaling with cluster size[J]. Journal of Computational Chemistry, 1999, 20(16): 1752-1759.
20	Oganov A R, Glass C W. Crystal structure prediction using ab initio evolutionary techniques: principles and applications[J]. The Journal of Chemical Physics, 2006, 124(24): 244704.
21	Shayeghi A, Götz D, Davis J B A, et al. Pool-BCGA: a parallelised generation-free genetic algorithm for the ab initio global optimisation of nanoalloy clusters[J]. Physical Chemistry Chemical Physics, 2015, 17(3): 2104-2112.
22	Zhang J, Hu P, Wang H. Amorphous catalysis: machine learning driven high-throughput screening of superior active site for hydrogen evolution reaction[J]. The Journal of Physical Chemistry C, 2020, 124(19): 10483-10494.
23	Zhong M, Tran K, Min Y, et al. Accelerated discovery of CO₂ electrocatalysts using active machine learning[J]. Nature, 2020, 581(7807): 178-183.
24	Bisbo M K, Hammer B. Efficient global structure optimization with a machine-learned surrogate model[J]. Physical Review Letters, 2020, 124(8): 086102.
25	Le T C, Winkler D A. Discovery and optimization of materials using evolutionary approaches[J]. Chemical Reviews, 2016, 116(10): 6107-6132.
26	Gobin O C, Schüth F. On the suitability of different representations of solid catalysts for combinatorial library design by genetic algorithms[J]. Journal of Combinatorial Chemistry, 2008, 10(6): 835-846.
27	Tipton W W, Hennig R G. A grand canonical genetic algorithm for the prediction of multi-component phase diagrams and testing of empirical potentials[J]. Journal of Physics: Condensed Matter, 2013, 25(49): 495401.
28	Rodemerck U, Baerns M, Holena M, et al. Application of a genetic algorithm and a neural network for the discovery and optimization of new solid catalytic materials[J]. Applied Surface Science, 2004, 223(1): 168-174.
29	Lv J, Wang Y, Zhu L, et al. Particle-swarm structure prediction on clusters[J]. The Journal of Chemical Physics, 2012, 137(8): 084104.
30	Lyakhov A O, Oganov A R, Stokes H T, et al. New developments in evolutionary structure prediction algorithm USPEX[J]. Computer Physics Communications, 2013, 184(4): 1172-1182.
31	Wang Y, Lv J, Zhu L, et al. CALYPSO: a method for crystal structure prediction[J]. Computer Physics Communications, 2012, 183(10): 2063-2070.
32	Zhai H, Alexandrova A N. Ensemble-average representation of Pt clusters in conditions of catalysis accessed through GPU accelerated deep neural network fitting global optimization[J]. Journal of Chemical Theory and Computation, 2016, 12(12): 6213-6226.
33	Hajinazar S, Sandoval E D, Cullo A J, et al. Multitribe evolutionary search for stable Cu–Pd–Ag nanoparticles using neural network models[J]. Physical Chemistry Chemical Physics, 2019, 21(17): 8729-8742.
34	Jennings P C, Lysgaard S, Hummelshøj J S, et al. Genetic algorithms for computational materials discovery accelerated by machine learning[J]. npj Computational Materials, 2019, 5(1): 46.
35	Curtis F, Li X, Rose T, et al. GAtor: a first-principles genetic algorithm for molecular crystal structure prediction[J]. Journal of Chemical Theory and Computation, 2018, 14(4): 2246-2264.
36	Maldonis J J, Xu Z, Song Z, et al. StructOpt: a modular materials structure optimization suite incorporating experimental data and simulated energies[J]. Computational Materials Science, 2019, 160: 1-8.
37	Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
38	Pereira S R M, Clerc F, Farrusseng D, et al. Effect of the genetic algorithm parameters on the optimisation of heterogeneous catalysts[J]. QSAR & Combinatorial Science, 2005, 24(1): 45-57.
39	Yee L, Yong G, Zong-Ben X. Degree of population diversity - a perspective on premature convergence in genetic algorithms and its Markov chain analysis[J]. IEEE Transactions on Neural Networks, 1997, 8(5): 1165-1176.
40	Rata I, Shvartsburg A A, Horoi M, et al. Single-parent evolution algorithm and the optimization of Si clusters[J]. Physical Review Letters, 2000, 85(3): 546-549.
41	Jäger M, Schäfer R, Johnston R L. GIGA: a versatile genetic algorithm for free and supported clusters and nanoparticles in the presence of ligands[J]. Nanoscale, 2019, 11(18): 9042-9052.
42	Jørgensen M S, Groves M N, Hammer B. Combining evolutionary algorithms with clustering toward rational global structure optimization at the atomic scale[J]. Journal of Chemical Theory and Computation, 2017, 13(3): 1486-1493.
43	Supady A, Blum V, Baldauf C. First-principles molecular structure search with a genetic algorithm[J]. Journal of Chemical Information and Modeling, 2015, 55(11): 2338-2348.
44	Davis J B A, Shayeghi A, Horswell S L, et al. The Birmingham parallel genetic algorithm and its application to the direct DFT global optimisation of Ir_N(N = 10–20) clusters[J]. Nanoscale, 2015, 7(33): 14032-14038.
45	Hussein H A, Demiroglu I, Johnston R L. Application of a parallel genetic algorithm to the global optimization of medium-sized Au–Pd sub-nanometre clusters[J]. The European Physical Journal B, 2018, 91(2): 34.
46	Demiroglu I, Yao K, Hussein H A, et al. DFT global optimization of gas-phase subnanometer Ru–Pt clusters[J]. The Journal of Physical Chemistry C, 2017, 121(20): 10773-10780.
47	Hussein H A, Davis J B A, Johnston R L. DFT global optimisation of gas-phase and MgO-supported sub-nanometre AuPd clusters[J]. Physical Chemistry Chemical Physics, 2016, 18(37): 26133-26143.
48	Habershon S, Harris K D M, Johnston R L. Development of a multipopulation parallel genetic algorithm for structure solution from powder diffraction data[J]. Journal of Computational Chemistry, 2003, 24(14): 1766-1774.
49	Fan T E, Shao G F, Ji Q S, et al. A multi-populations multi-strategies differential evolution algorithm for structural optimization of metal nanoclusters[J]. Computer Physics Communications, 2016, 208: 64-72.
50	Jiang B, Li J, Guo H. Potential energy surfaces from high fidelity fitting of ab initio points: the permutation invariant polynomial - neural network approach[J]. International Reviews in Physical Chemistry, 2016, 35(3): 479-506.
51	Li H, Zhang Z, Liu Z. Application of artificial neural networks for catalysis: a review[J]. Catalysts, 2017, 7(10): 306.
52	Le T, Epa V C, Burden F R, et al. Quantitative structure-property relationship modeling of diverse materials properties[J]. Chemical Reviews, 2012, 112(5): 2889-2919.
53	Kamath A, Vargas-Hernández R A, Krems R V, et al. Neural networks vs Gaussian process regression for representing potential energy surfaces: a comparative study of fit quality and vibrational spectrum accuracy[J]. The Journal of Chemical Physics, 2018, 148(24): 241702.
54	Chmiela S, Tkatchenko A, Sauceda H E, et al. Machine learning of accurate energy-conserving molecular force fields[J]. Science Advances, 2017, 3(5): e1603015.
55	Chen X, Jørgensen M S, Li J, et al. Atomic energies from a convolutional neural network[J]. Journal of Chemical Theory and Computation, 2018, 14(7): 3933-3942.
56	Rupp M, Tkatchenko A, Müller K R, et al. Fast and accurate modeling of molecular atomization energies with machine learning[J]. Physical Review Letters, 2012, 108(5): 058301.
57	Ramakrishnan R, Dral P O, Rupp M, et al. Quantum chemistry structures and properties of 134 kilo molecules[J]. Scientific Data, 2014, 1(1): 140022.
58	Behler J. Constructing high-dimensional neural network potentials: a tutorial review[J]. International Journal of Quantum Chemistry, 2015, 115(16): 1032-1050.
59	Zhang L, Lin D Y, Wang H, et al. Active learning of uniformly accurate interatomic potentials for materials simulation[J]. Physical Review Materials, 2019, 3(2): 023804.
60	Kolsbjerg E L, Peterson A A, Hammer B. Neural-network-enhanced evolutionary algorithm applied to supported metal nanoparticles[J]. Physical Review B, 2018, 97(19): 195424.
61	Sørensen K H, Jørgensen M S, Bruix A, et al. Accelerating atomic structure search with cluster regularization[J]. The Journal of Chemical Physics, 2018, 148(24): 241734.
62	Jørgensen M S, Larsen U F, Jacobsen K W, et al. Exploration versus exploitation in global atomistic structure optimization[J]. The Journal of Physical Chemistry A, 2018, 122(5): 1504-1509.
63	Grosan C, Abraham A. Hybrid Evolutionary Algorithms: Methodologies, Architectures, and Reviews [M]. Berlin, Heidelberg: Springer-Verlag, 2007: 1-17.
64	Chen P H, Shahandashti S M. Hybrid of genetic algorithm and simulated annealing for multiple project scheduling with multiple resource constraints[J]. Automation in Construction, 2009, 18(4): 434-443.
65	Zacharias C R, Lemes M R, Dal Pino A. Combining genetic algorithm and simulated annealing: a molecular geometry optimization study[J]. Journal of Molecular Structure: THEOCHEM, 1998, 430: 29-39.
66	Cai W, Jiang H, Shao X. Global optimization of lennard-jones clusters by a parallel fast annealing evolutionary algorithm[J]. Journal of Chemical Information and Computer Sciences, 2002, 42(5): 1099-1103.
67	Zeiri Y. Study of the lowest energy structure of atomic clusters using a genetic algorithm[J]. Computer Physics Communications, 1997, 103(1): 28-42.
68	Alexandrova A N, Boldyrev A I. Search for the Li_n⁰/⁺¹/^-1 (n = 5-7) lowest-energy structures using the ab initio gradient embedded genetic algorithm (GEGA). Elucidation of the chemical bonding in the lithium clusters[J]. Journal of Chemical Theory and Computation, 2005, 1(4): 566-580.
69	Dieterich J M, Hartke B. OGOLEM: global cluster structure optimisation for arbitrary mixtures of flexible molecules. A multiscaling, object-oriented approach[J]. Molecular Physics, 2010, 108(3/4): 279-291.
70	Vargas J A, Buendía F, Beltrán M R. New Au_N (N = 27–30) lowest energy clusters obtained by means of an improved DFT–genetic algorithm methodology[J]. The Journal of Physical Chemistry C, 2017, 121(20): 10982-10991.
71	Yamazoe S, Koyasu K, Tsukuda T. Nonscalable oxidation catalysis of gold clusters[J]. Accounts of Chemical Research, 2013, 47(3): 816-824.
72	Assadollahzadeh B, Schwerdtfeger P. A systematic search for minimum structures of small gold clusters Au_n (n=2–20) and their electronic properties[J]. The Journal of Chemical Physics, 2009, 131(6): 064306.
73	Li T X, Yin S Y, Ji Y L, et al. A genetic algorithm study on the most stable disordered and ordered configurations of Au_38–55[J]. Physics Letters A, 2000, 267(5/6): 403-407.
74	Shayeghi A, Johnston R L, Schäfer R. Evaluation of photodissociation spectroscopy as a structure elucidation tool for isolated clusters: a case study of Ag⁴⁺ and Au⁴⁺[J]. Physical Chemistry Chemical Physics, 2013, 15(45): 19715-19723.
75	Gilb S, Weis P, Furche F, et al. Structures of small gold cluster cations (Au_n⁺, n<14): ion mobility measurements versus density functional calculations[J]. The Journal of Chemical Physics, 2002, 116(10): 4094-4101.
76	Hong L, Wang H, Cheng J, et al. Atomic structures and electronic properties of small Au–Ag binary clusters: effects of size and composition[J]. Computational and Theoretical Chemistry, 2012, 993: 36-44.
77	Kang X, Li Y, Zhu M, et al. Atomically precise alloy nanoclusters: syntheses, structures, and properties[J]. Chemical Society Reviews, 2020, 49: 6443-6514.
78	Xie S, Tsunoyama H, Kurashige W, et al. Enhancement in aerobic alcohol oxidation catalysis of Au₂₅ clusters by single Pd atom doping[J]. ACS Catalysis, 2012, 2(7): 1519-1523.
79	Liu C, Ren X, Lin F, et al. Structure of the Au_23-_xAg_x(S-Adm)₁₅ nanocluster and its application for photocatalytic degradation of organic pollutants[J]. Angewandte Chemie International Edition, 2019, 58(33): 11335-11339.
80	Heiles S, Logsdail A J, Schäfer R, et al. Dopant-induced 2D–3D transition in small Au-containing clusters: DFT-global optimisation of 8-atom Au–Ag nanoalloys[J]. Nanoscale, 2012, 4(4): 1109-1115.
81	Davis J B A, Horswell S L, Johnston R L. Global optimization of 8–10 atom palladium–iridium nanoalloys at the DFT level[J]. The Journal of Physical Chemistry A, 2013, 118(1): 208-214.
82	Heard C J, Johnston R L. A density functional global optimisation study of neutral 8-atom Cu-Ag and Cu-Au clusters[J]. The European Physical Journal D, 2013, 67(2): 34.
83	Luo Z, Nachammai V, Zhang B, et al. Toward understanding the growth mechanism: tracing all stable intermediate species from reduction of Au(I)–thiolate complexes to evolution of Au₂₅ nanoclusters[J]. Journal of the American Chemical Society, 2014, 136(30): 10577-10580.
84	Hussein H A, Demiroglu I, Johnston R L. Application of a parallel genetic algorithm to the global optimization of medium-sized Au–Pd sub-nanometre clusters[J]. The European Physical Journal B, 2018, 91(2): 34.
85	Bailey M S, Wilson N T, Roberts C, et al. Structures, stabilities and ordering in Ni-Al nanoalloy clusters[J]. The European Physical Journal D - Atomic, Molecular, Optical and Plasma Physics, 2003, 25(1): 41-55.
86	Zhang J, Glezakou V A, Rousseau R, et al. NWPEsSe: an adaptive-learning global optimization algorithm for nanosized cluster systems[J]. Journal of Chemical Theory and Computation, 2020, 16(6): 3947-3958.
87	Sierka M, Todorova T K, Kaya S, et al. Interplay between theory and experiment in the quest for silica with reduced dimensionality grown on a Mo(112) surface[J]. Chemical Physics Letters, 2006, 424(1/2/3): 115-119.
88	Hjorth L A, Jørgen M J, Blomqvist J, et al. The atomic simulation environment—a Python library for working with atoms[J]. Journal of Physics: Condensed Matter, 2017, 29(27): 273002.
89	Vilhelmsen L B, Walton K S, Sholl D S. Structure and mobility of metal clusters in MOFs: Au, Pd, and AuPd clusters in MOF-74[J]. Journal of the American Chemical Society, 2012, 134(30): 12807-12816.
90	He Y, Liu J C, Luo L, et al. Size-dependent dynamic structures of supported gold nanoparticles in CO oxidation reaction condition[J]. Proceedings of the National Academy of Sciences, 2018, 115(30): 7700-7705.
91	Sun G, Alexandrova A N, Sautet P. Pt₈ cluster on alumina under a pressure of hydrogen: support-dependent reconstruction from first-principles global optimization[J]. The Journal of Chemical Physics, 2019, 151(19): 194703.
92	Vilhelmsen L B, Hammer B. Systematic study of Au₆ to Au₁₂ gold clusters on MgO(100) F-centers using density-functional theory[J]. Physical Review Letters, 2012, 108(12): 126101.

[1]	程业品, 胡达清, 徐奕莎, 刘华彦, 卢晗锋, 崔国凯. 离子液体基低共熔溶剂在转化CO₂中的应用[J]. 化工学报, 2023, 74(9): 3640-3653.
[2]	陈杰, 林永胜, 肖恺, 杨臣, 邱挺. 胆碱基碱性离子液体催化合成仲丁醇性能研究[J]. 化工学报, 2023, 74(9): 3716-3730.
[3]	宋明昊, 赵霏, 刘淑晴, 李国选, 杨声, 雷志刚. 离子液体脱除模拟油中挥发酚的多尺度模拟与研究[J]. 化工学报, 2023, 74(9): 3654-3664.
[4]	杨学金, 杨金涛, 宁平, 王访, 宋晓双, 贾丽娟, 冯嘉予. 剧毒气体PH₃的干法净化技术研究进展[J]. 化工学报, 2023, 74(9): 3742-3755.
[5]	胡建波, 刘洪超, 胡齐, 黄美英, 宋先雨, 赵双良. 有机笼跨细胞膜易位行为的分子动力学模拟研究[J]. 化工学报, 2023, 74(9): 3756-3765.
[6]	赵佳佳, 田世祥, 李鹏, 谢洪高. SiO₂-H₂O纳米流体强化煤尘润湿性的微观机理研究[J]. 化工学报, 2023, 74(9): 3931-3945.
[7]	范孝雄, 郝丽芳, 范垂钢, 李松庚. LaMnO₃/生物炭催化剂低温NH₃-SCR催化脱硝性能研究[J]. 化工学报, 2023, 74(9): 3821-3830.
[8]	李艺彤, 郭航, 陈浩, 叶芳. 催化剂非均匀分布的质子交换膜燃料电池操作条件研究[J]. 化工学报, 2023, 74(9): 3831-3840.
[9]	吴雷, 刘姣, 李长聪, 周军, 叶干, 刘田田, 朱瑞玉, 张秋利, 宋永辉. 低阶粉煤催化微波热解制备含碳纳米管的高附加值改性兰炭末[J]. 化工学报, 2023, 74(9): 3956-3967.
[10]	胡兴枝, 张皓焱, 庄境坤, 范雨晴, 张开银, 向军. 嵌有超小CeO₂纳米粒子的碳纳米纤维的制备及其吸波性能[J]. 化工学报, 2023, 74(8): 3584-3596.
[11]	杨菲菲, 赵世熙, 周维, 倪中海. Sn掺杂的In₂O₃催化CO₂选择性加氢制甲醇[J]. 化工学报, 2023, 74(8): 3366-3374.
[12]	李凯旋, 谭伟, 张曼玉, 徐志豪, 王旭裕, 纪红兵. 富含零价钴活性位点的钴氮碳/活性炭设计及甲醛催化氧化应用研究[J]. 化工学报, 2023, 74(8): 3342-3352.
[13]	杨欣, 彭啸, 薛凯茹, 苏梦威, 吴燕. 分子印迹-TiO₂光电催化降解增溶PHE废水性能研究[J]. 化工学报, 2023, 74(8): 3564-3571.
[14]	汪林正, 陆俞冰, 张睿智, 罗永浩. 基于分子动力学模拟的VOCs热氧化特性分析[J]. 化工学报, 2023, 74(8): 3242-3255.
[15]	陈吉, 洪泽, 雷昭, 凌强, 赵志刚, 彭陈辉, 崔平. 基于分子动力学的焦炭溶损反应及其机理研究[J]. 化工学报, 2023, 74(7): 2935-2946.